单选题
1、已知全集U=R,A={x|x≥1},B={x|-1
答 案:A
解 析:补集运算应明确知道是否包括端点.A在U中的补集是x<1, 


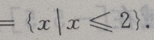
2、已知向量a=(3,4),向量 b=(0,-2),则cos的值为()
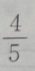
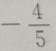

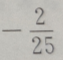
答 案:B
解 析:求cos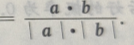 a·b=(3,4)·(0,-2)=3×0+4×(-2)=8,
a·b=(3,4)·(0,-2)=3×0+4×(-2)=8,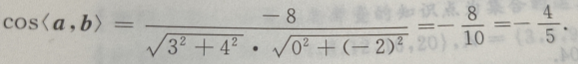
3、将一颗骰子抛掷1次,到的点数为偶数的概率为

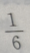

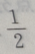
答 案:D
解 析:一颗骰子的点数分别为1,2,3,4,5,6,其中偶数与奇数各占一半,故抛掷1次,得到的点数为偶数的概率为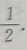
4、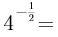 ( )
( )
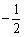
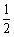
答 案:C
主观题
1、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得 AB=120m,求河的宽
AB=120m,求河的宽

答 案:如图,  ∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD= =60m,
即河宽为60m
=60m,
即河宽为60m
2、已知数列 的前n项和
的前n项和 求证:
求证: 是等差数列,并求公差和首项。
是等差数列,并求公差和首项。
答 案:

3、设函数f(x)=xlnx+x.(I)求曲线y=f(x)在点((1,f(1))处的切线方程;
(II)求f(x)的极值.
答 案:(I)f(1)=1,f'(x)=2+lnx,故f'(1)=2.所以曲线y=f(x)在点(1,f(1))处的切线方程为y=2x-1.(II)令f'(x)=0,解得 当
当 时,f'(x)
时,f'(x) 单调递减,在区间
单调递减,在区间 单调递增.因此f(x)在
单调递增.因此f(x)在 时取得极小值
时取得极小值
4、在△ABC中,B=120°,BC=4,△ABC的面积为 ,求AC.
,求AC.
答 案:由△ABC的面积为 得
得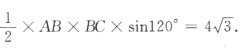 所以AB =4.因此
所以AB =4.因此 所以
所以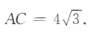
填空题
1、 的展开式是()
的展开式是()
答 案: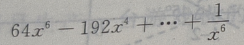
解 析: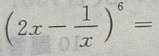
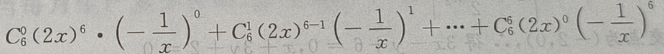

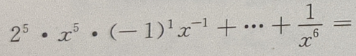
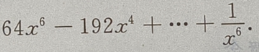
2、lg(tan43°tan45°tan47°)=()
答 案:0
解 析:lg(tan43°tan45°tan47°)=lg(tan43°tan45°cot43°)=lgtan45°=lg1=0