单选题
1、函数f(x)= 当x∈[-2,+∞)时是增函数,当x∈(-∞,-2]时是减函数,则f(1)=()
当x∈[-2,+∞)时是增函数,当x∈(-∞,-2]时是减函数,则f(1)=()
答 案:B
解 析:由题意知抛物线的对称轴为x=-2, 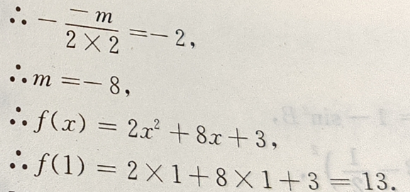
2、设M=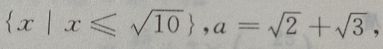 那么()
那么()
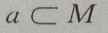
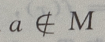
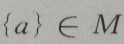
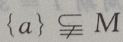
答 案:D
解 析: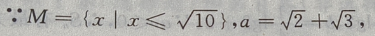 M是集合,a为元素,{a}为集合,元素与集合的关系是
M是集合,a为元素,{a}为集合,元素与集合的关系是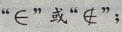 集合与集合的关系是
集合与集合的关系是

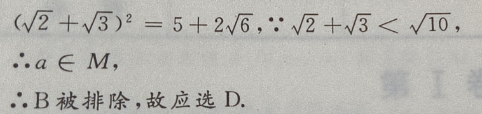
3、函数f(x)=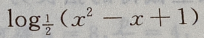 的单调增区间是()
的单调增区间是()
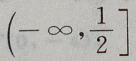
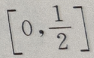

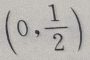
答 案:A
解 析: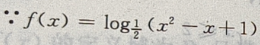 中的
中的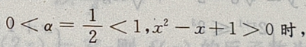
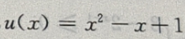 的减区间就为f(x)的增区间,设u(x)=
的减区间就为f(x)的增区间,设u(x)=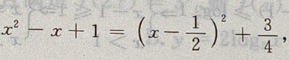 当x∈R时,u(x)>0,函数u(x)在
当x∈R时,u(x)>0,函数u(x)在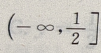 是减函数,
是减函数, 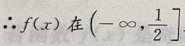 上是增函数
故f(x)=
上是增函数
故f(x)=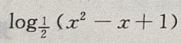 的单调增区间为
的单调增区间为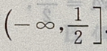 ps:关于复合函数的问题要逐步分清每一层次的函数的图像和性质,再结合起来考虑整体,有时也可画出部分函数的图像来帮助分析和理解.
ps:关于复合函数的问题要逐步分清每一层次的函数的图像和性质,再结合起来考虑整体,有时也可画出部分函数的图像来帮助分析和理解.
4、函数 与y
与y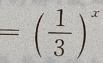 的图像之间的关系是
的图像之间的关系是
答 案:D
解 析: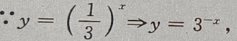
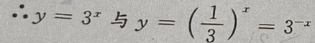 关于y轴对称,
关于y轴对称,
主观题
1、设函数f(x)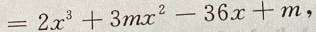 且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
答 案:(Ⅰ)由已知得f'=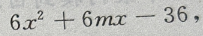 又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=
又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=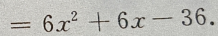 令f'(x)=0,解得
令f'(x)=0,解得 当x<-3时,f'(x)>0;
当-3
当x<-3时,f'(x)>0;
当-3
2、如图:已知在△ADC中,∠C=90°,∠D=30°,∠ABC=45°,BD=20,求AC(用小数表示,保留一位小数)

答 案:如图 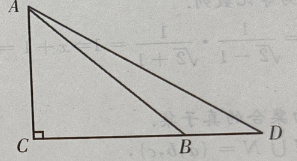
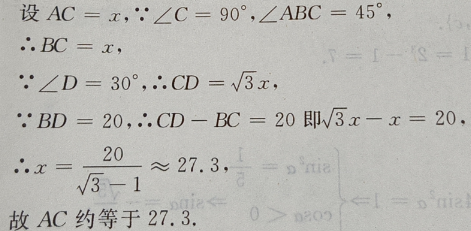
3、已知等差数列 前n项和
前n项和 (Ⅰ)求通项
(Ⅰ)求通项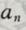 的表达式
(Ⅱ)求
的表达式
(Ⅱ)求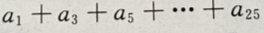 的值
的值
答 案:(Ⅰ)当n=1时,由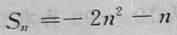 得
得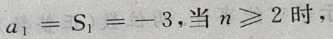
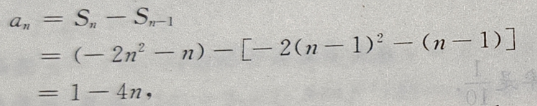
 也满足上式,故
也满足上式,故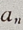 =1-4n(n≥1)
(Ⅱ)由于数列
=1-4n(n≥1)
(Ⅱ)由于数列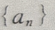 是首项为
是首项为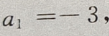 公差为d=-4的等差数列,所以
公差为d=-4的等差数列,所以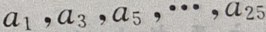 是首项为
是首项为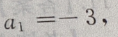 公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:
公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:

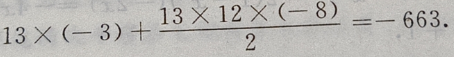
4、已知三角形的一个内角是 ,面积是
,面积是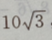 周长是20,求各边的长.
周长是20,求各边的长.
答 案:设三角形三边分别为a,b,c,∠A=60°, 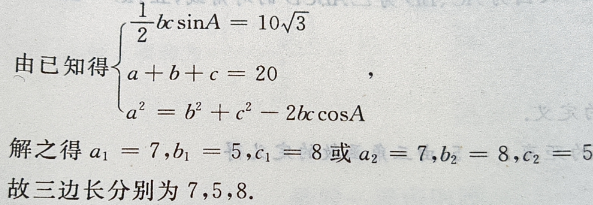
填空题
1、函数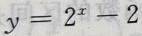 的图像与坐轴的交点共有()个
的图像与坐轴的交点共有()个
答 案:2
解 析:当x=0, 故函数与y轴交于(0,-1)点;令y=0,则有
故函数与y轴交于(0,-1)点;令y=0,则有 故函数与工轴交于(1,0)点,因此函数
故函数与工轴交于(1,0)点,因此函数 与坐标轴的交点共有2个
与坐标轴的交点共有2个
2、函数f(x)=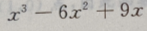 在区间[-3,3]上的最大值为()
在区间[-3,3]上的最大值为()
答 案:4
解 析:这题考的是高次函数的最值问题,可用导数来求函数在区间[-3,3]上的最值。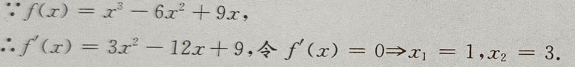 列出表格
列出表格 由上表可知函数在[-3,3]上,在x=1点处有最大值为4.
由上表可知函数在[-3,3]上,在x=1点处有最大值为4.