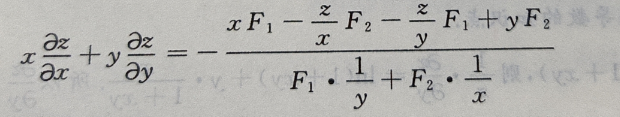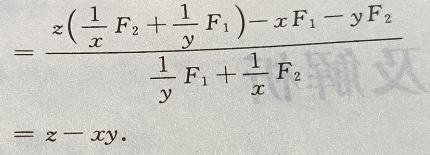单选题
1、用待定系数法求微分方程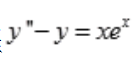 的一个特解时,特解的形式是().(式中a、b是常数)
的一个特解时,特解的形式是().(式中a、b是常数)


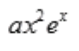
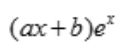
答 案:A
解 析:y″-y=0的特征方程是r2-1=0,特征根为r1=1,r2=-1.y″-y=xex中自由项f(x)=xex,a=1是特征单根,则特解为y*=x(ax+b)ex=(ax2+bx)ex。
2、级数 (k为非零常数)()。
(k为非零常数)()。
答 案:C
解 析:级数各项取绝对值得级数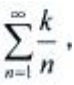 为发散级数;由莱布尼茨判别法可知
为发散级数;由莱布尼茨判别法可知 收敛,故
收敛,故 为条件收敛。
为条件收敛。
3、若函数F(x)和G(x)都是函数f(x)的原函数,则下列四个式子,正确的是()。

答 案:D
解 析: 。
。
主观题
1、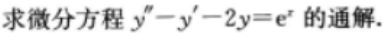
答 案:
2、计算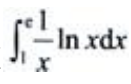 .
.
答 案:解:
3、求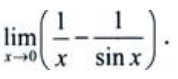
答 案:解: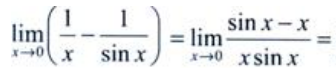
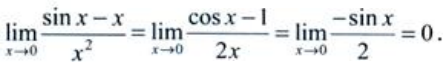
填空题
1、设I=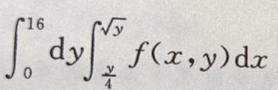 交换积分次序,则有I=()
交换积分次序,则有I=()
答 案: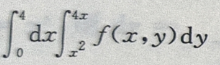
解 析: 的积分区域
的积分区域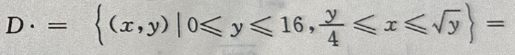
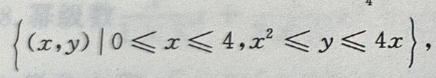
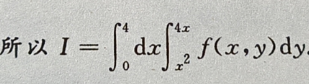
2、过原点且垂直于y轴的平面方程为()。
答 案:y=0
解 析:过原点且垂直于y轴的平面即x轴所在的平面,方程为y=0。
3、设 ,则f(x)=()。
,则f(x)=()。
答 案:6x2
解 析:对题设方程两边求导,即得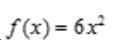 。
。
简答题
1、设函数z(x,y)由方程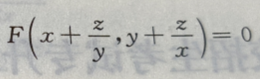 所确定
证明:
所确定
证明: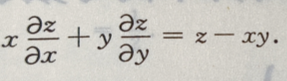
答 案: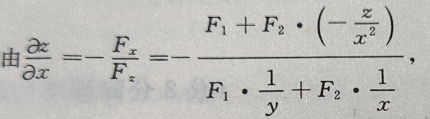
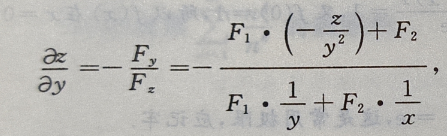 所以
所以