单选题
1、已知向量i,j为互相垂直的单位向量,向量a=2i+mj,若|a|=2,则m=()
答 案:C
解 析:由题可知a=(2,m),因此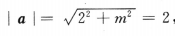 ,故m=0.
,故m=0.
2、在△ABC中,三边为a、b、c,∠B=60°,则 的值是()
的值是()
答 案:C
解 析:由已知用余弦定理得: 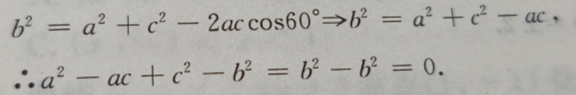
3、函数y=2sinxcosx的最小正周期是()
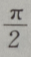

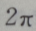

答 案:D
解 析:y=2sinxcosx=sin2x,故其最小正周期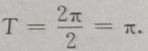
4、从15名学生中选出两人担任正、副班长,不同的选举结果共有()
答 案:C
解 析:由已知条件可知本题属于排列问题,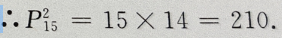
主观题
1、每亩地种果树20棵时,每棵果树收入90元,如果每亩增种一棵,每棵果树收入就下降3元,求使总收入最大的种植棵数.
答 案:设每亩增种x棵,总收入味y元,则每亩种树(20+x)棵,由题意知增种x棵后每棵收入为(60-3x) 则有y=(90-3x)(20+x)
整理得y=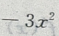 +30x+1800
配方得y=
+30x+1800
配方得y= +1875
当x=5时,y有最大值,所以每亩地最多种25棵
+1875
当x=5时,y有最大值,所以每亩地最多种25棵
2、在△ABC中,B=120°,C=30°,BC=4,求△ABC的面积.
答 案:因为A= 180°-B-C=30°,所以AB = BC=4.因此△ABC的面积
3、已知三角形的一个内角是 ,面积是
,面积是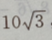 周长是20,求各边的长.
周长是20,求各边的长.
答 案:设三角形三边分别为a,b,c,∠A=60°, 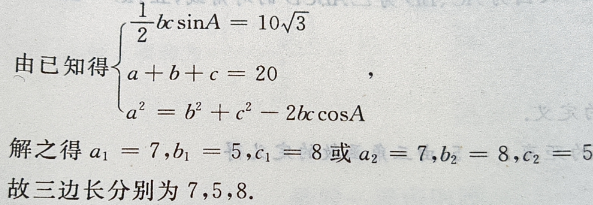
4、设函数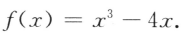
(I)求f'(2);
(II)求f(x)在区间[一1,2]的最大值与最小值.
答 案:(I)因为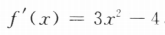 ,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.
,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.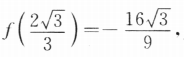 f(2)=0.
f(2)=0.
所以f(x)在区间[一1,2]的最大值为3,最小值为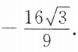
填空题
1、函数y=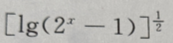 的定义域是()
的定义域是()
答 案:[1,+∞)
解 析:要是函数y= 有意义,需使
有意义,需使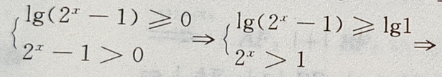
 所以函数的定义域为{x|x≥1}=[1,+∞)
所以函数的定义域为{x|x≥1}=[1,+∞)
2、任选一个不大于20的正整数,它恰好是3的整数倍的概率是()
答 案: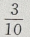
解 析:设n为不大于20的正整数的个数,则n=20,m为在这20个数中3的倍数:3,6、9、12、15、18的个数。 ∴m=6,∴所求概率=