单选题
1、函数y=x2+1(x>0)的图像在()
答 案:A
解 析:当x>0时,函数y=x2+1>0,因此函数的图像在第一象限.
2、用1,2,3,4一组成没有重复数字的三位数,其中偶数共有()
答 案:B
解 析:若三位数为偶数,个位数只能从2,4中选一个,故没有重复数字的偶数三位数为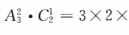
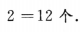
3、函数f(x)= 当x∈[-2,+∞)时是增函数,当x∈(-∞,-2]时是减函数,则f(1)=()
当x∈[-2,+∞)时是增函数,当x∈(-∞,-2]时是减函数,则f(1)=()
答 案:B
解 析:由题意知抛物线的对称轴为x=-2, 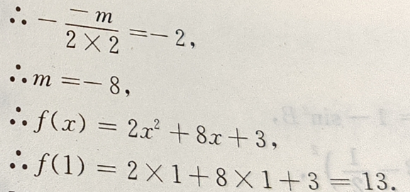
4、若向量a=(1,-1),b=(1,x),且|a+b|=2,则x=()。
答 案:C
解 析: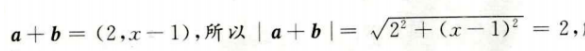 解得x=1 本题主要考查的知识点为向量的加法和模。
解得x=1 本题主要考查的知识点为向量的加法和模。
主观题
1、已知三角形的一个内角是 ,面积是
,面积是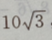 周长是20,求各边的长.
周长是20,求各边的长.
答 案:设三角形三边分别为a,b,c,∠A=60°, 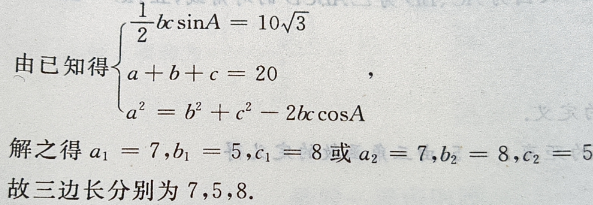
2、已知函数f(x)=(x-4)(x2-a)。(I)求f’(x);
(Ⅱ)若f’(-1)=8,求f(x)在区间[0,4]的最大值与最小值。
答 案:(I)f'(x) =(x-4)'(x2-a)+(x-4)(x2-a)’
=x2-a+2x(x-4)
=3x2-8x-a.
(Ⅱ)由于f’(-1)=3+8-a=8,得a=3.
令f'(x)=3x2-8x-3=0,解得x1=3, (舍去)又f(0)=12,f(3)=-6,f(4)=0所以在区间[0,4]上函数最大值为12,最小值为-6
(舍去)又f(0)=12,f(3)=-6,f(4)=0所以在区间[0,4]上函数最大值为12,最小值为-6
3、已知等差数列{an}中,a1+a3+a5=6,a2+a4+a6=12,求{an}的首项与公差.
答 案:因为{an}为等差数列,则
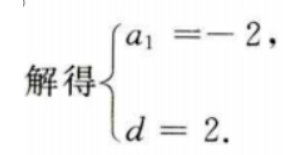
4、在△ABC中,AB=2,BC=3,B=60°,求AC及△ABC的面积
答 案:
填空题
1、过点(2,0)作圆x2+y2=1的切线,切点的横坐标为()。
答 案: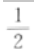
解 析:本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有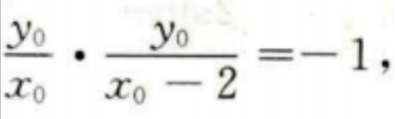 即
即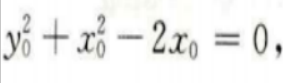
 所以
所以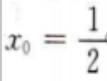 故切点横坐标为
故切点横坐标为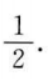
2、已知向量a=(3,2),b=(-4,x),且a⊥b,则x=()
答 案:6
解 析:∵a⊥b, ∴3×(-4)+2x=0 ∴x=6.