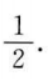单选题
1、直线2x-y+7=0,与圆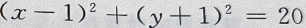 的位置关系是()
的位置关系是()
答 案:C
解 析:易知圆心坐标(1,-1),圆心到直线2x-y+7=0的距离d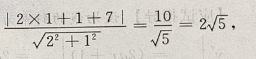 ∵圆的半径
∵圆的半径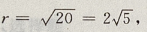 ∴d=r,∴直线与圆相切
∴d=r,∴直线与圆相切

2、函数f(x)=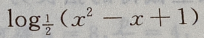 的单调增区间是()
的单调增区间是()
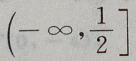
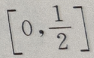

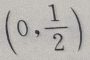
答 案:A
解 析: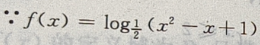 中的
中的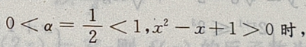
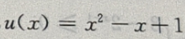 的减区间就为f(x)的增区间,设u(x)=
的减区间就为f(x)的增区间,设u(x)=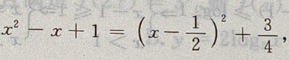 当x∈R时,u(x)>0,函数u(x)在
当x∈R时,u(x)>0,函数u(x)在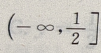 是减函数,
是减函数, 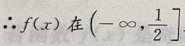 上是增函数
故f(x)=
上是增函数
故f(x)=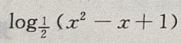 的单调增区间为
的单调增区间为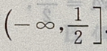 ps:关于复合函数的问题要逐步分清每一层次的函数的图像和性质,再结合起来考虑整体,有时也可画出部分函数的图像来帮助分析和理解.
ps:关于复合函数的问题要逐步分清每一层次的函数的图像和性质,再结合起来考虑整体,有时也可画出部分函数的图像来帮助分析和理解.
3、设α是三角形的一个内角,若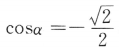 ,则sinα=()
,则sinα=()
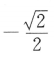
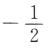
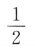
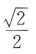
答 案:D
解 析:由题知0<α<兀,而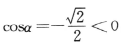 ,故
,故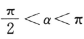 ,因此
,因此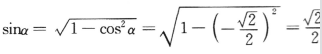 .
.
4、袋中有6个球,其中4个红球,2个白球,从中随机取出2个球,则这2个球都为红球的概率为()
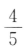
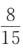
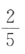

答 案:C
解 析:两个球都是红球的概率为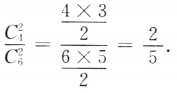
主观题
1、设椭圆的中心是坐标原点,长轴在x轴上,离心率 已知点P
已知点P 到圆上的点的最远距离是
到圆上的点的最远距离是 求椭圆的方程
求椭圆的方程
答 案:由题意,设椭圆方程为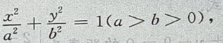 由
由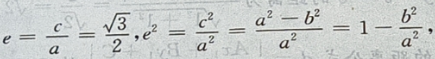
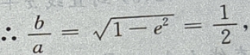 设P
设P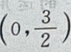 点到椭圆上任一点的距离为 d,
点到椭圆上任一点的距离为 d,
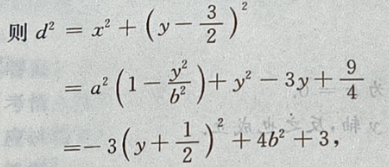
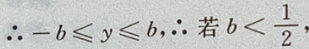 则在y=-b时,
则在y=-b时,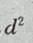 最大,即d也最大。
最大,即d也最大。
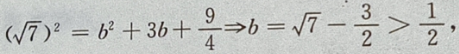

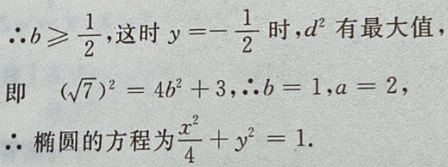
2、设函数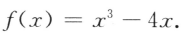
(I)求f'(2);
(II)求f(x)在区间[一1,2]的最大值与最小值.
答 案:(I)因为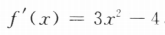 ,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.
,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.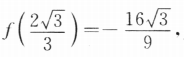 f(2)=0.
f(2)=0.
所以f(x)在区间[一1,2]的最大值为3,最小值为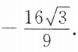
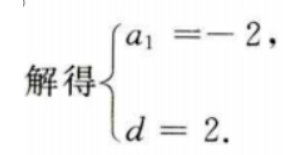
3、已知等差数列{an}中,a1+a3+a5=6,a2+a4+a6=12,求{an}的首项与公差.
答 案:因为{an}为等差数列,则
4、设函数f(x)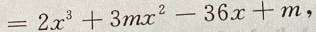 且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
答 案:(Ⅰ)由已知得f'=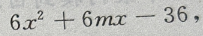 又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=
又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=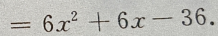 令f'(x)=0,解得
令f'(x)=0,解得 当x<-3时,f'(x)>0;
当-3
当x<-3时,f'(x)>0;
当-3
填空题
1、从某班的一次数学测试卷中任意抽出10份,其得分情况如下:81,98,43,75,60,55,78,84,90,70,则这次测验成绩的样本方差是()
答 案:252.84
解 析:
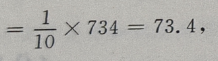
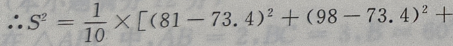
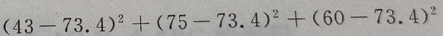
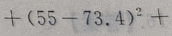
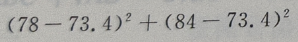
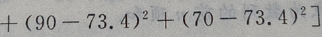 =252.84
=252.84
2、过点(2,0)作圆x2+y2=1的切线,切点的横坐标为()。
答 案: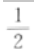
解 析:本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有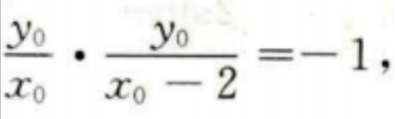 即
即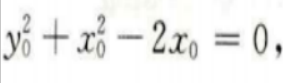
 所以
所以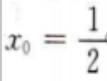 故切点横坐标为
故切点横坐标为