单选题
1、若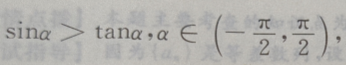 则
则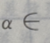 ()
()


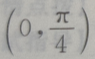
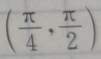
答 案:B
解 析:首先做出单位圆,然后根据问题的约束条件,利用三角函数线找出满足条件的a角取值范围 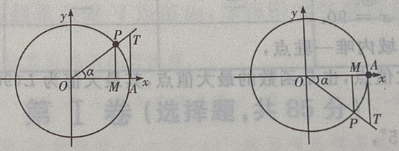
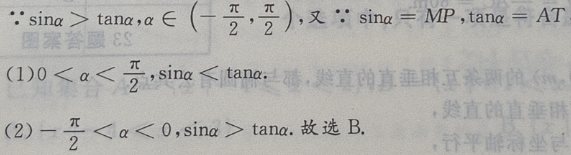
2、在等比数列{an}中,a2=1,公比q=2,则a5=()。
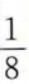
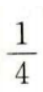
答 案:D
解 析:本题主要考查的知识点为等比数列。
3、圆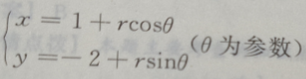 的圆心在()点上
的圆心在()点上
答 案:A
解 析:因为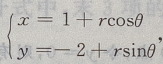 所以圆的圆心为O(1,-2)
所以圆的圆心为O(1,-2)
4、函数y=-x2+2x的值域是()。
答 案:C
解 析:本题主要考查的知识点为函数的值域. y=-x2+2x=1-(x-1)2≤1,故原函数的值域为(-∞,1]
主观题
1、某工厂每月生产x台游戏机的收入为R(x)= +130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
+130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
答 案:利润 =收入-成本, L(x)=R(x)-C(x)= +130x-206-(50x+100)=
+130x-206-(50x+100)=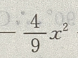 +80x-306
法一:用二次函数
+80x-306
法一:用二次函数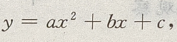 当a<0时有最大值
当a<0时有最大值
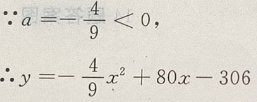 是开口向下的抛物线,有最大值
是开口向下的抛物线,有最大值
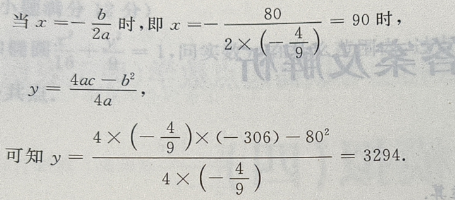 法二:用导数来求解
法二:用导数来求解
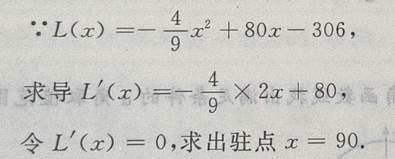 因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
2、在正四棱柱ABCD-A'B'C'D'中, (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证:
答 案:(Ⅰ)由题意知(如图所示) 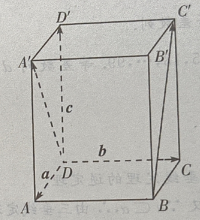
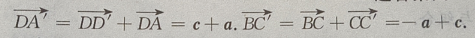
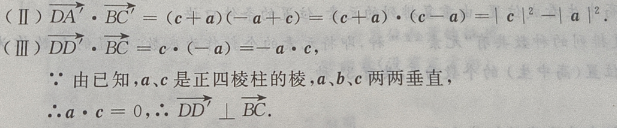
3、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。 (I)求C的方程; (Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB
答 案:(I)由题意,该抛物线的焦点到准线的距离为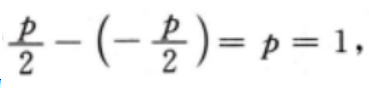 所以抛物线C的方程为
所以抛物线C的方程为 (Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得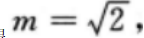 因此A点坐标为
因此A点坐标为 设B点坐标为
设B点坐标为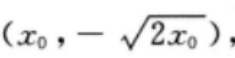 则
则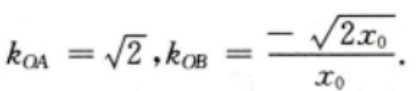 因为
因为 则有
则有 即
即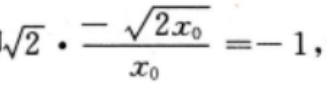 解得x0=4
所以B点的坐标为
解得x0=4
所以B点的坐标为
4、建筑一个容积为8000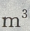 ,深为6m的长方体蓄水池,池壁每
,深为6m的长方体蓄水池,池壁每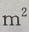 的造价为15元,池底每
的造价为15元,池底每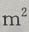 的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
答 案: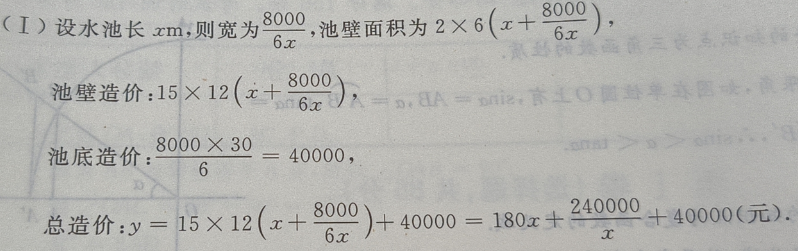

填空题
1、函数y=-x2+ax图像的对称轴为x=2,则a=______。
答 案:4
解 析:本题主要考查的知识点为二次函数的性质
由题意,该函数图像的对称轴为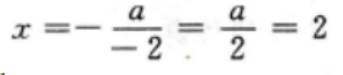
2、函数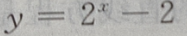 的图像与坐标轴的交点共有()
的图像与坐标轴的交点共有()
答 案:2
解 析:当x=0时,y=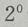 -2=-1,故函数与y轴交于(0,-1)点,令y=0,则有
-2=-1,故函数与y轴交于(0,-1)点,令y=0,则有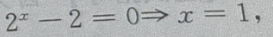 故函数与x轴交于(1,0) 点,因此函数
故函数与x轴交于(1,0) 点,因此函数 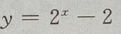 与坐标轴的交点共有 2个.
与坐标轴的交点共有 2个.