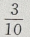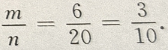单选题
1、若x 答 案：D 解 析：本题主要考查的知识点为不等式的性质。 因为 2、函数 答 案：D 解 析： 3、不等式|2x-3|≤1的解集为（） 答 案：A 解 析： 4、函数y=-x2+2x的值域是（）。
答 案：C 解 析：本题主要考查的知识点为函数的值域.
y=-x2+2x=1-(x-1)2≤1，故原函数的值域为(-∞,1] 主观题 1、在△ABC中，B=120°,C=30°,BC=4，求△ABC的面积． 答 案：因为A= 180°-B-C=30°，所以AB = BC=4.因此△ABC的面积 2、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)
答 案：如图 3、已知直线l的斜率为1，l过抛物线C： 答 案：(I）C的焦点为 4、每亩地种果树20棵时,每棵果树收入90元,如果每亩增种一棵,每棵果树收入就下降3元,求使总收入最大的种植棵数.
答 案：设每亩增种x棵,总收入味y元，则每亩种树(20+x)棵，由题意知增种x棵后每棵收入为（60-3x） 则有y=(90-3x)(20+x)
整理得y= 填空题 1、函数 答 案：2 解 析：当x=0， 2、任选一个不大于20的正整数,它恰好是3的整数倍的概率是（）
答 案： 解 析：设n为不大于20的正整数的个数,则n=20,m为在这20个数中3的倍数:3,6、9、12、15、18的个数。 ∴m=6，∴所求概率=
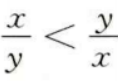
与y
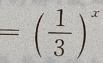的图像之间的关系是
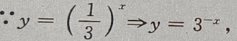
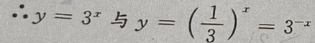关于y轴对称，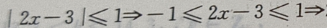
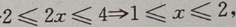故原不等式的解集为{x|1≤x≤2}
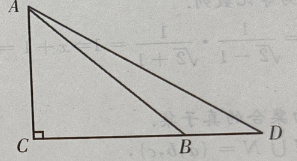
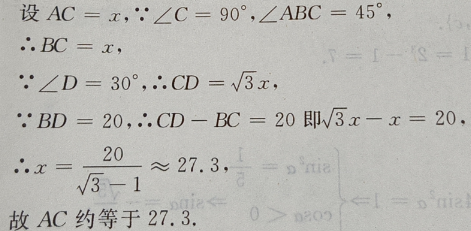
的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．
，准线为
由题意得l的方程为
因此l与C的准线的交点坐标为
(II）由
得
设A（x1,y1）.B（x2,y2），则
因此
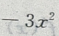+30x+1800
配方得y=
+1875
当x=5时，y有最大值，所以每亩地最多种25棵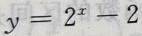
的图像与坐轴的交点共有（）个
故函数与y轴交于(0,-1)点;令y=0,则有
故函数与工轴交于(1,0)点,因此函数
与坐标轴的交点共有2个
