单选题
1、已知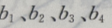 成等差数列,且
成等差数列,且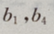 为方程
为方程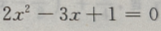 的两个根,则
的两个根,则 的值为()
的值为()


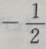
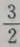
答 案:D
解 析:由根与系数的关系得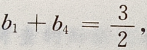 由等差数列的性质得
由等差数列的性质得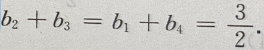
2、若函数y=f(x)在[-1,1]上是单调函数,则使得y=f(sinx)必为单调函数的区间是()

答 案:C
解 析:y=f(x)在[-1,1]上是单调函数,所以y=f(x)的单调区间为[-1,1] 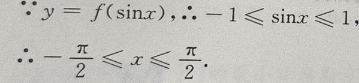
3、一个袋子中装有标号分别为1,2,3,4的四个球,采用有放回的方式从袋中摸球两次,每次摸出一个球,则恰有一次摸出2号球的概率为()。
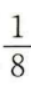

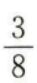

答 案:C
解 析:本题主要考查的知识点为独立重复试验的概率。 所求概率为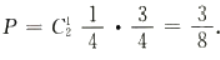
4、已知向量a=(3,4),b=(0,-2),则cos=()

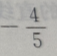
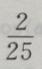
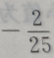
答 案:B
解 析:因为a=(3,4),b=(0,-2), 
主观题
1、已知三角形的一个内角是 ,面积是
,面积是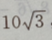 周长是20,求各边的长.
周长是20,求各边的长.
答 案:设三角形三边分别为a,b,c,∠A=60°, 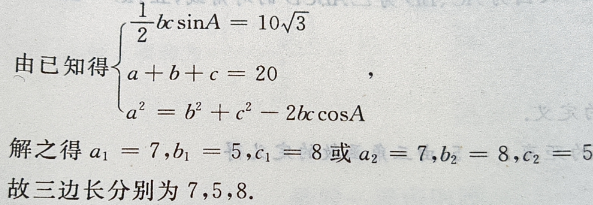
2、每亩地种果树20棵时,每棵果树收入90元,如果每亩增种一棵,每棵果树收入就下降3元,求使总收入最大的种植棵数.
答 案:设每亩增种x棵,总收入味y元,则每亩种树(20+x)棵,由题意知增种x棵后每棵收入为(60-3x) 则有y=(90-3x)(20+x)
整理得y=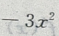 +30x+1800
配方得y=
+30x+1800
配方得y= +1875
当x=5时,y有最大值,所以每亩地最多种25棵
+1875
当x=5时,y有最大值,所以每亩地最多种25棵
3、设椭圆的中心是坐标原点,长轴在x轴上,离心率 已知点P
已知点P 到圆上的点的最远距离是
到圆上的点的最远距离是 求椭圆的方程
求椭圆的方程
答 案:由题意,设椭圆方程为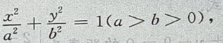 由
由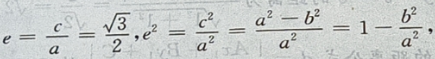
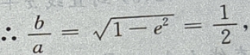 设P
设P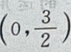 点到椭圆上任一点的距离为 d,
点到椭圆上任一点的距离为 d,
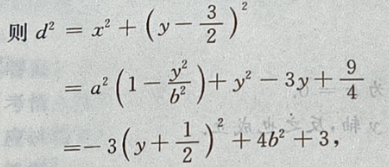
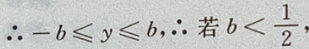 则在y=-b时,
则在y=-b时,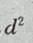 最大,即d也最大。
最大,即d也最大。
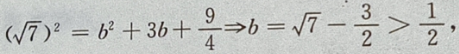

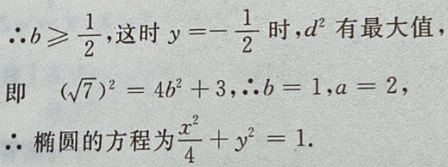
4、已知函数f(x)=(x-4)(x2-a)。(I)求f’(x);
(Ⅱ)若f’(-1)=8,求f(x)在区间[0,4]的最大值与最小值。
答 案:(I)f'(x) =(x-4)'(x2-a)+(x-4)(x2-a)’
=x2-a+2x(x-4)
=3x2-8x-a.
(Ⅱ)由于f’(-1)=3+8-a=8,得a=3.
令f'(x)=3x2-8x-3=0,解得x1=3, (舍去)又f(0)=12,f(3)=-6,f(4)=0所以在区间[0,4]上函数最大值为12,最小值为-6
(舍去)又f(0)=12,f(3)=-6,f(4)=0所以在区间[0,4]上函数最大值为12,最小值为-6
填空题
1、函数f(x)=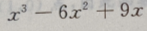 在区间[-3,3]上的最大值为()
在区间[-3,3]上的最大值为()
答 案:4
解 析:这题考的是高次函数的最值问题,可用导数来求函数在区间[-3,3]上的最值。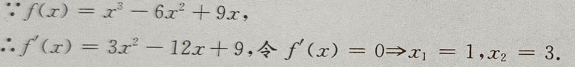 列出表格
列出表格 由上表可知函数在[-3,3]上,在x=1点处有最大值为4.
由上表可知函数在[-3,3]上,在x=1点处有最大值为4.
2、函数y=-x²+ax图像的对称轴为x=2,则a=______。
答 案:4
解 析:本题主要考查的知识点为二次函数的性质。 由题意,该函数图像的对称轴为 得a=4。
得a=4。