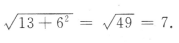单选题
1、设双曲线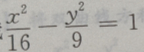
的渐近线的斜率为k，则|k|=（）
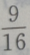
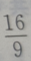
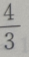
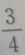
答 案：D
解 析：双曲线渐近线的斜率为k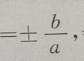
故本题中k
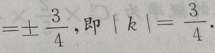
2、已知集合M =(2,3,5,a),N =(1,3,4,b),若M∩N=(1,2,3),则a,b的值为
答 案：C
解 析：M∩N={2,3,5,a} ∩{1,3,4,6} ={1,2,3} 又因为M中无“1”元素，而有“a”元素，只有a=1 而N中无“2”元素，而有“b元素”，只有b=2
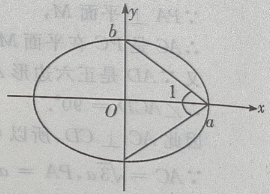
3、从椭圆与x轴额右交点看短轴两端点的视角为60°的椭圆的离心率（）
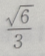
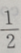
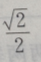
答 案：A
解 析：求椭圆的离心率,先求出a,c.(如图) 
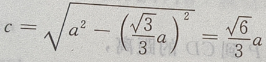，由椭圆定义知
4、过点P(2,3)且在两轴上截距相等的直线方程为()
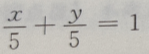
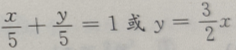
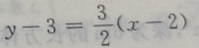
答 案：B
解 析：选项A中，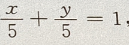
在x、y 轴上截距为 5.但答案不完整 所以选项B中有两个方程，
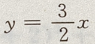在x轴上横截距与y轴上的纵截距都为0，也是相等的
选项C,虽然过点(2,3),实质上与选项A相同.选项 D,转化为: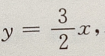
答案不完整
主观题
1、设函数f(x)=
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
答 案：(Ⅰ)函数的定义域为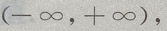
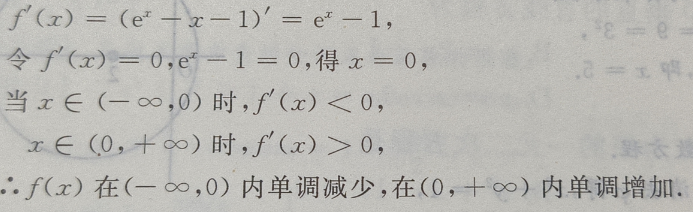(Ⅱ)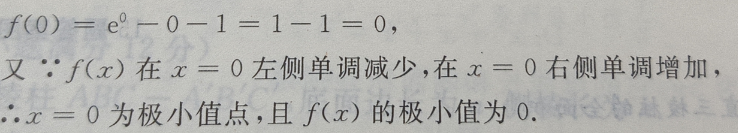
2、已知数列
的前n项和
求证：
是等差数列，并求公差和首项。
答 案：
3、已知等差数列前n项和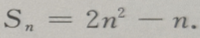
（Ⅰ）求这个数列的通项公式;（Ⅱ）求数列第六项到第十项的和
答 案：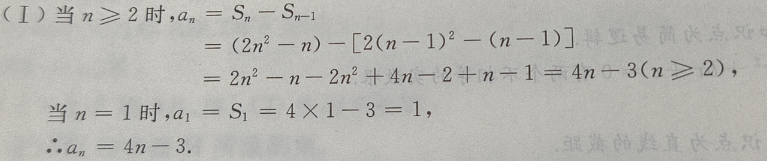
4、建筑一个容积为8000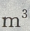
,深为6m的长方体蓄水池，池壁每
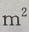的造价为15元，池底每
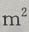的造价为30元。（I）把总造价y(元)表示为长x(m)的函数；（Ⅱ）求函数的定义域
答 案：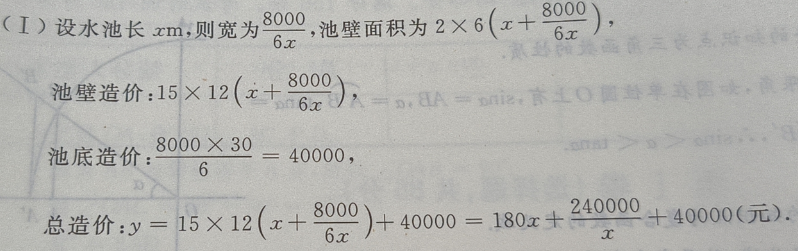
填空题
1、函数
的定义域是（）
答 案：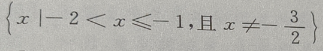
解 析：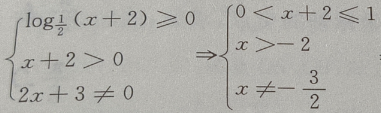
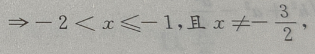所以函数
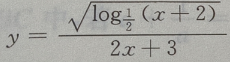的定义域是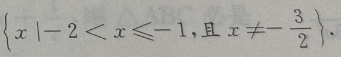
2、长方体的长、宽、高分别为2,3,6，则该长方体的对角线长为（）
答 案：7
解 析：由题可知长方体的底面的对角线长为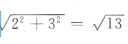
，则在由高、底面对角线、长方体的对角线组成的三角形中，长方体的对角线长为
