单选题
1、b=0是直线y=kx+b过原点的()
答 案:C
解 析:b=0 直线y=kx+b过原点
直线y=kx+b过原点
2、已知双曲线上一点到两焦点(-5,0),(5,0)距离之差的绝对值等于6,则双曲线方程为()
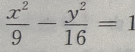
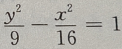
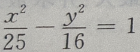
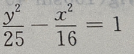
答 案:A
解 析:由已知条件知双曲线焦点在x轴上属于第一类标准式,又知c=5,2a=6, ∴a=3,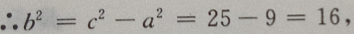 ∴所求双曲线的方程为
∴所求双曲线的方程为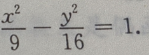
3、函数y=2sinxcosx的最小正周期是()


答 案:D
解 析:y=2sinxcosx=sin2x,故其最小正周期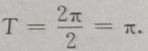
4、函数f(x)= 当x∈[-2,+∞)时是增函数,当x∈(-∞,-2]时是减函数,则f(1)=()
当x∈[-2,+∞)时是增函数,当x∈(-∞,-2]时是减函数,则f(1)=()
答 案:B
解 析:由题意知抛物线的对称轴为x=-2, 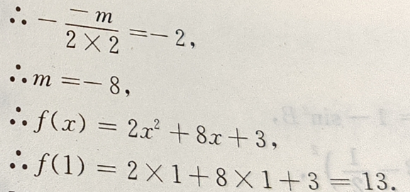
主观题
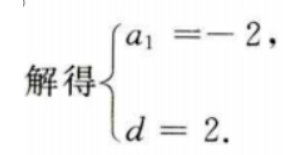
1、已知等差数列{an}中,a1+a3+a5=6,a2+a4+a6=12,求{an}的首项与公差.
答 案:因为{an}为等差数列,则
2、设函数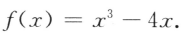
(I)求f'(2);
(II)求f(x)在区间[一1,2]的最大值与最小值.
答 案:(I)因为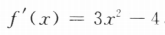 ,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.
,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.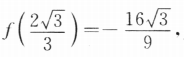 f(2)=0.
f(2)=0.
所以f(x)在区间[一1,2]的最大值为3,最小值为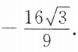
3、在△ABC中,AB=2,BC=3,B=60°,求AC及△ABC的面积
答 案:
4、设椭圆的中心是坐标原点,长轴在x轴上,离心率 已知点P
已知点P 到圆上的点的最远距离是
到圆上的点的最远距离是 求椭圆的方程
求椭圆的方程
答 案:由题意,设椭圆方程为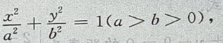 由
由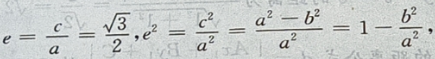
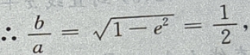 设P
设P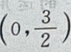 点到椭圆上任一点的距离为 d,
点到椭圆上任一点的距离为 d,
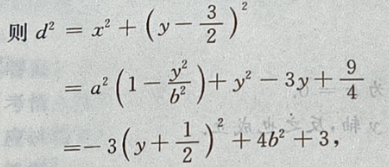
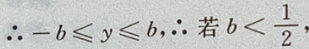 则在y=-b时,
则在y=-b时,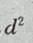 最大,即d也最大。
最大,即d也最大。
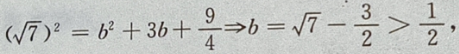

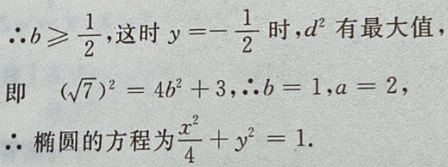
填空题
1、已知向量a=(3,2),b=(-4,x),且a⊥b,则x=()
答 案:6
解 析:∵a⊥b, ∴3×(-4)+2x=0 ∴x=6.
2、曲线在点(1,1)处的切线方程是______。
答 案:2x+y-3=0
解 析:本题主要考查的知识点为切线方程。
由题意,该切线斜率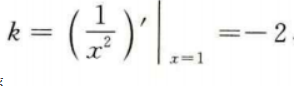 ,又过点(1,1),所以切线方程为y-1=-2(x-1),即2x+y-3=0。
,又过点(1,1),所以切线方程为y-1=-2(x-1),即2x+y-3=0。