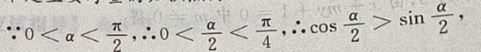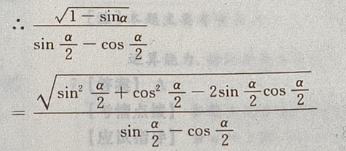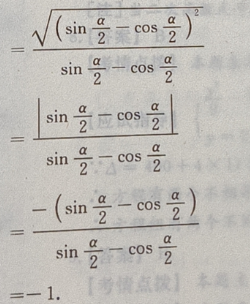单选题
1、甲袋内有2个白球3个黑球,乙袋内有3个白球1个黑球,现从两个袋内各摸出1个球,摸出的两个球都是白球的概率是
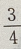
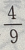
答 案：C
解 析：由已知条件可知此题属于相互独立同时发生的事件，从甲袋内摸到白球的概率为P(A)=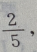
乙袋内摸到白球的概率为
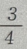，所以现从两袋中各提出一个球，摸出的两个都是白球的概率为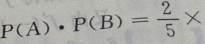
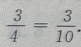
2、袋中有6个球，其中4个红球，2个白球，从中随机取出2个球，则这2个球都为红球的概率为（）
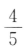
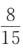
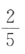
答 案：C
解 析：两个球都是红球的概率为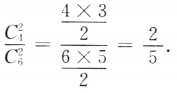
3、函数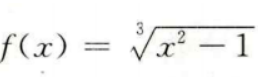
的定义域为（）。
答 案：A
解 析：本题主要考查的知识点为函数的定义域。 对于
奇次根号下无要求，故函数的定义域为R。
4、一个袋子中装有标号分别为1，2，3，4的四个球，采用有放回的方式从袋中摸球两次，每次摸出一个球，则恰有一次摸出2号球的概率为（）。
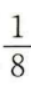
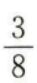
答 案：C
解 析：本题主要考查的知识点为独立重复试验的概率。 所求概率为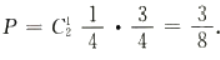
主观题
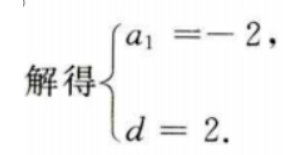
1、已知等差数列{an}中，a1+a3+a5=6，a2+a4+a6=12，求{an}的首项与公差.
答 案：因为{an}为等差数列，则
2、已知直线l的斜率为1，l过抛物线C：
的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．
答 案：(I）C的焦点为
，准线为
由题意得l的方程为
因此l与C的准线的交点坐标为
(II）由
得
设A（x1,y1）.B（x2,y2），则
因此
3、在△ABC中,已知三边 a、b、c 成等差数列,且最大角∠A是最小角的2倍, a: b :c.
答 案：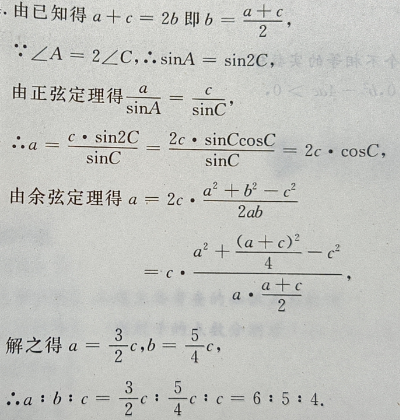
4、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。
答 案：(I)由题意,该抛物线的焦点到准线的距离为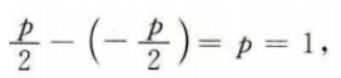
所以抛物线C的方程为y2=2x.
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得 m=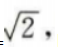
因此A点坐标为
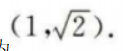设B点坐标为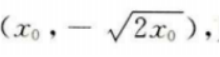
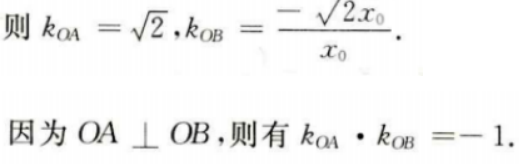
填空题
1、从某班的一次数学测试卷中任意抽出10份,其得分情况如下:81,98,43,75,60,55,78,84,90,70,则这次测验成绩的样本方差是（）
答 案：252.84
解 析：
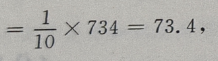
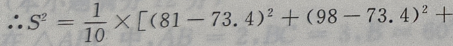
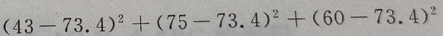
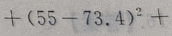
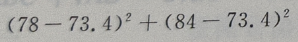
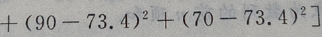=252.84
2、设
则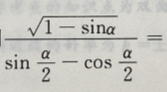
答 案：-1
解 析：
