单选题
1、下列函数中,为增函数的是()。
答 案:A
解 析:本题主要考查的知识点为函数的单调性. 对于y=x3,y’=3x2≥0,故y=x3为增函数
2、设α是第三象限角,若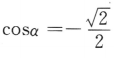 ,则sinα=()
,则sinα=()
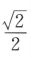

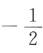
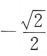
答 案:D
解 析:由于 ,而α为第三象限角,故
,而α为第三象限角,故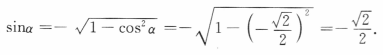
3、已知点M(1,2),N(2,3),则直线MN的斜率为()。
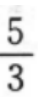
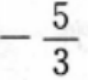
答 案:B
解 析:本题主要考查的知识点为直线的斜率.
直线MN的斜率为: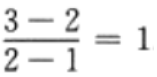
4、给出下列两个命题:①如果一条直线与一个平面垂直,则该直线与该平面内的任意一条直线垂直②以二面角的棱上任意一点为端点,在二面角的两个面内分别作射线,则这两条射线所成的角为该二面角的平面角.则()
答 案:B
解 析:一条直线与平面垂直,则直线与平面内的任意一条直线垂直,故①为真命题;二面角的两条射线必须垂直于二面角的棱,故②为假命题,因此选B选项.
主观题
1、某工厂每月生产x台游戏机的收入为R(x)= +130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
+130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
答 案:利润 =收入-成本, L(x)=R(x)-C(x)= +130x-206-(50x+100)=
+130x-206-(50x+100)=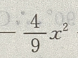 +80x-306
法一:用二次函数
+80x-306
法一:用二次函数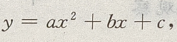 当a<0时有最大值
当a<0时有最大值
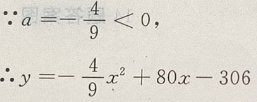 是开口向下的抛物线,有最大值
是开口向下的抛物线,有最大值
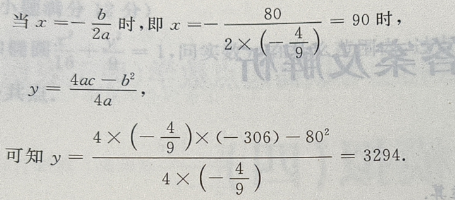 法二:用导数来求解
法二:用导数来求解
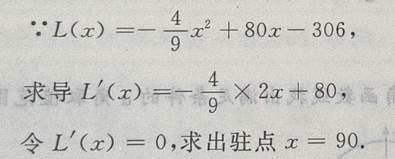 因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
2、建筑一个容积为8000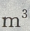 ,深为6m的长方体蓄水池,池壁每
,深为6m的长方体蓄水池,池壁每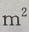 的造价为15元,池底每
的造价为15元,池底每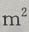 的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
答 案: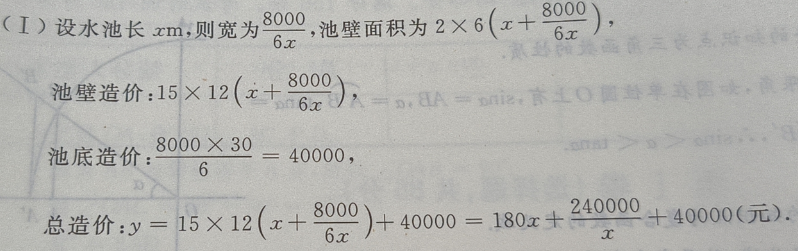

3、设函数f(x)= (Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
答 案:(Ⅰ)函数的定义域为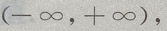
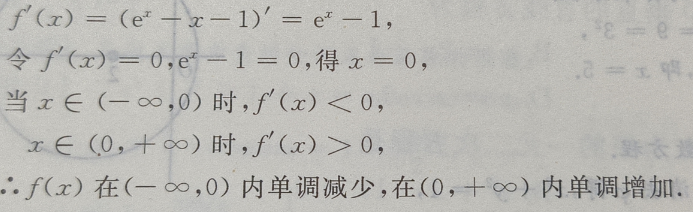 (Ⅱ)
(Ⅱ)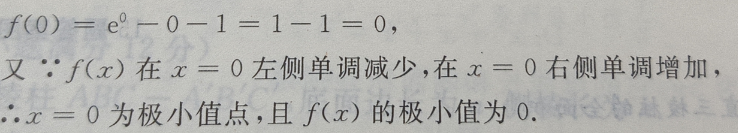
4、已知a,b,c成等差数列,a,b,c+1成等比数列.若b=6,求a和c.
答 案:由已知得 解得
解得
填空题
1、lg(tan43°tan45°tan47°)=()
答 案:0
解 析:lg(tan43°tan45°tan47°)=lg(tan43°tan45°cot43°)=lgtan45°=lg1=0
2、九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。
答 案:85
解 析:本题主要考查的知识点为中位数. 将成绩按由小到大排列:63,77,79,81,85,88,89,94,99.因此中位数为85。