单选题
1、设z=x2y,则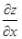 =()。
=()。
答 案:B
解 析: 。
。
2、设f(0)=0,且f'(0)存在,则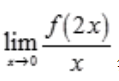 等于()。
等于()。
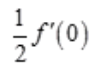
答 案:A
解 析: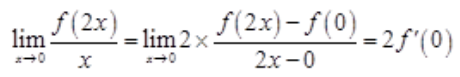 。
。
3、设函数f(x)在(0,1)上可导且在[0,1]上连续,且f'(x)>0,f(0)<0,f(1)>0,则f(x)在(0,1)内()。
答 案:B
解 析:因为函数f(x)在[0,1]上连续,f(0)<0,f(1)>0,故存在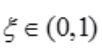 ,使得
,使得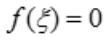 ,又f'(x)>0,函数在(0,1)上单调增加,故f(x)在(0,1)内有且仅有一个零点。
,又f'(x)>0,函数在(0,1)上单调增加,故f(x)在(0,1)内有且仅有一个零点。
主观题
1、求微分方程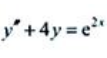 的通解。
的通解。
答 案:解: 的特征方程为
的特征方程为 ,则特征根为
,则特征根为 ,故其通解为
,故其通解为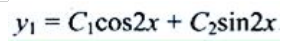 因为自由项
因为自由项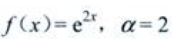 不是特征根,故设特殊解为
不是特征根,故设特殊解为 代入原方程,有
代入原方程,有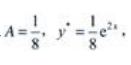 故
故 的通解为
的通解为
2、求 .
.
答 案:解: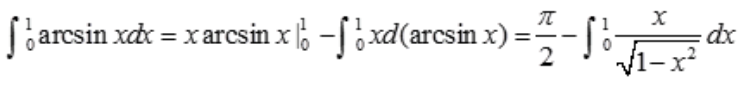 =
=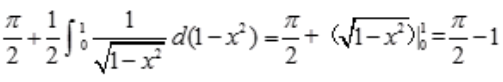 。
。
3、判断级数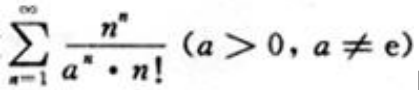 的敛散性。
的敛散性。
答 案:解:令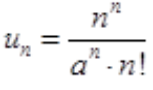 ,则
,则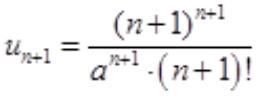 ,由于
,由于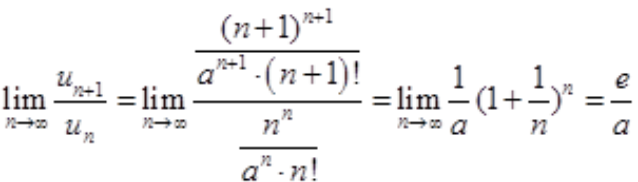 故有当
故有当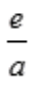 <1,即a>e时,该级数收敛;当
<1,即a>e时,该级数收敛;当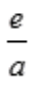 >1,即a<e时,该级数发散。
>1,即a<e时,该级数发散。
填空题
1、设D为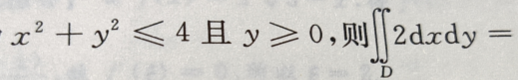 ()
()
答 案:
解 析:因积分区域为圆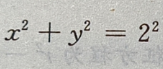 的上半圆,则
的上半圆,则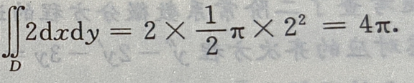
2、幂级数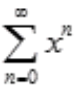 的收敛半径为()。
的收敛半径为()。
答 案:1
解 析: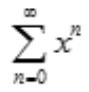 是最基本的幂级数之一,an=1,
是最基本的幂级数之一,an=1, ,故收敛半径为1。
,故收敛半径为1。
3、设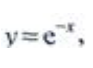 则y''=()。
则y''=()。
答 案:e-x
解 析: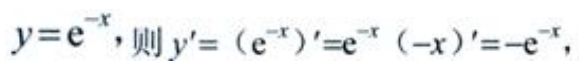
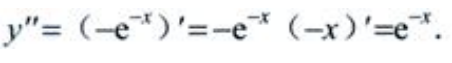
简答题
1、若函数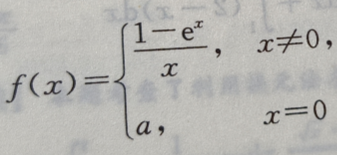 在x=0处连续。求a。
在x=0处连续。求a。
答 案:由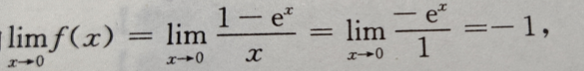 又因f(0)=a,所以当a=-1时,f(x)在x=0连续。
又因f(0)=a,所以当a=-1时,f(x)在x=0连续。