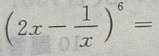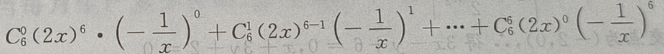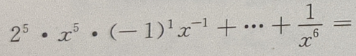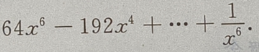单选题
1、若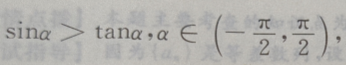 则
则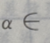 ()
()


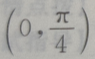
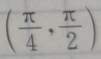
答 案:B
解 析:首先做出单位圆,然后根据问题的约束条件,利用三角函数线找出满足条件的a角取值范围 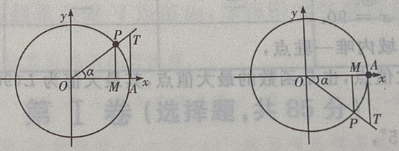
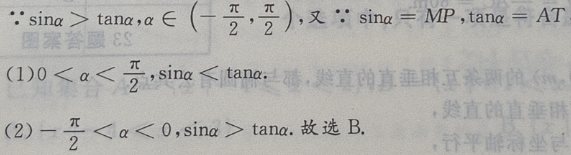
2、已知全集U=R,A={x|x≥1},B={x|-1
答 案:A
解 析:补集运算应明确知道是否包括端点.A在U中的补集是x<1, 


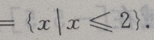
3、若向量a=(1,-1),b=(1,x),且|a+b|=2,则x=()。
答 案:C
解 析: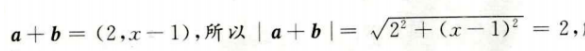 解得x=1 本题主要考查的知识点为向量的加法和模。
解得x=1 本题主要考查的知识点为向量的加法和模。
4、若x<y<0,则()。
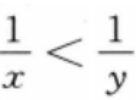
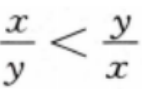

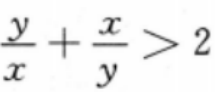
答 案:D.
解 析:本题主要考查的知识点为不等式的性质.
因为x<y<0,故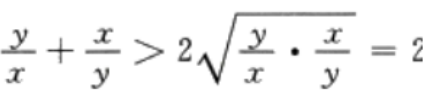
主观题
1、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 ,得
,得 设A(x1,y1),B(x2,y2),则
设A(x1,y1),B(x2,y2),则 因此
因此
2、在正四棱柱ABCD-A'B'C'D'中, (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证:
答 案:(Ⅰ)由题意知(如图所示) 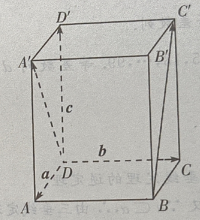
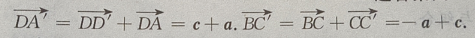
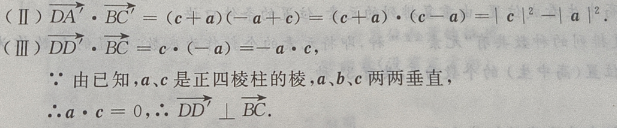
3、设函数f(x)=xlnx+x.(I)求曲线y=f(x)在点((1,f(1))处的切线方程;
(II)求f(x)的极值.
答 案:(I)f(1)=1,f'(x)=2+lnx,故f'(1)=2.所以曲线y=f(x)在点(1,f(1))处的切线方程为y=2x-1.(II)令f'(x)=0,解得 当
当 时,f'(x)
时,f'(x) 单调递减,在区间
单调递减,在区间 单调递增.因此f(x)在
单调递增.因此f(x)在 时取得极小值
时取得极小值
4、已知数列 的前n项和
的前n项和 求证:
求证: 是等差数列,并求公差和首项。
是等差数列,并求公差和首项。
答 案:

填空题
1、函数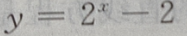 的图像与坐标轴的交点共有()
的图像与坐标轴的交点共有()
答 案:2
解 析:当x=0时,y=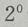 -2=-1,故函数与y轴交于(0,-1)点,令y=0,则有
-2=-1,故函数与y轴交于(0,-1)点,令y=0,则有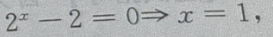 故函数与x轴交于(1,0) 点,因此函数
故函数与x轴交于(1,0) 点,因此函数 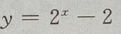 与坐标轴的交点共有 2个.
与坐标轴的交点共有 2个.
2、 的展开式是()
的展开式是()
答 案: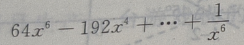
解 析: