单选题
1、已知函数f(x)的定义域为R，且满足f(2x)=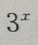
,则f(x)的反函数为（）
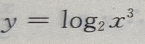
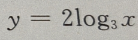
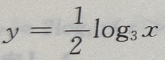
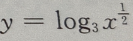
答 案：B
解 析：令2x=t，则x=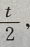
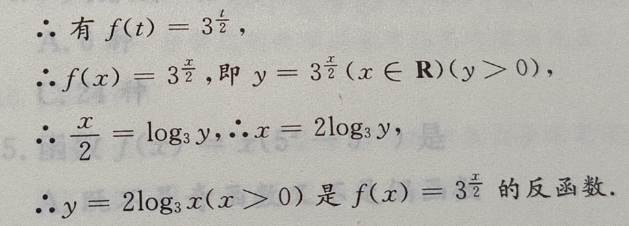
2、函数
的图像与直线y=4的交点坐标为（）
答 案：C
解 析：令y=4x=4，解得x=1，故所求交点为（1,4).
3、已知
，则sin2α=（）
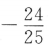
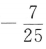
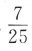
答 案：D
解 析：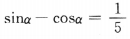
两边平方得
，故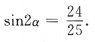
4、不等式|2x-3|≤1的解集为（）
答 案：A
解 析：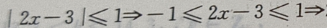
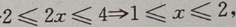故原不等式的解集为{x|1≤x≤2}
主观题
1、已知等差数列
前n项和
（Ⅰ）求通项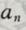
的表达式
（Ⅱ）求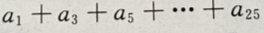
的值
答 案：（Ⅰ）当n=1时，由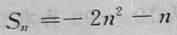
得
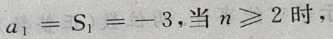
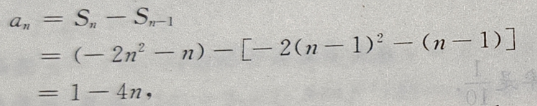
也满足上式，故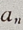
=1-4n（n≥1）
（Ⅱ）由于数列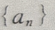
是首项为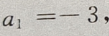
公差为d=-4的等差数列，所以
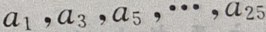是首项为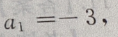
公差为d=-8，项数为13的等差数列，于是由等差数列前n项和公式得：
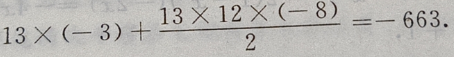
2、在△ABC中，B=120°,C=30°,BC=4，求△ABC的面积．
答 案：因为A= 180°-B-C=30°，所以AB = BC=4.因此△ABC的面积
3、已知函数f（x）=（x-4）（x2-a）。（I）求f’（x）；
（Ⅱ）若f’（-1）=8，求f（x）在区间[0，4]的最大值与最小值。
答 案：(I)f'(x) =(x-4)'(x2-a)+(x-4)(x2-a)’
=x2-a+2x(x-4)
=3x2-8x-a.
(Ⅱ)由于f’(-1)=3+8-a=8,得a=3.
令f'(x)=3x2-8x-3=0,解得x1=3，
（舍去）又f（0）=12，f（3）=-6，f（4）=0所以在区间[0，4]上函数最大值为12，最小值为-6
4、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。
答 案：(I)由题意,该抛物线的焦点到准线的距离为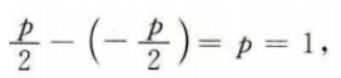
所以抛物线C的方程为y2=2x.
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得 m=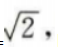
因此A点坐标为
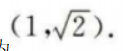设B点坐标为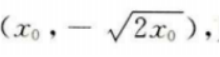
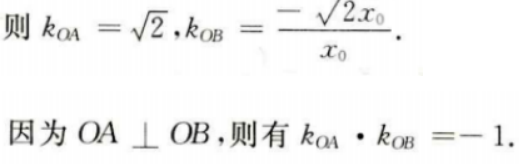
填空题
1、设
则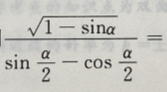
答 案：-1
解 析：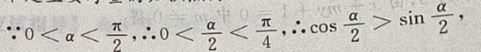
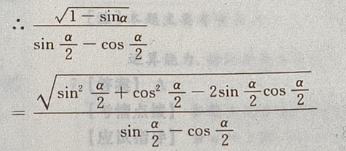
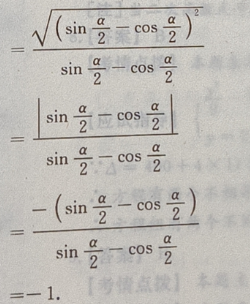
2、函数y=-x²+ax图像的对称轴为x=2，则a=______。
答 案：4
解 析：本题主要考查的知识点为二次函数的性质。 由题意，该函数图像的对称轴为
得a=4。
