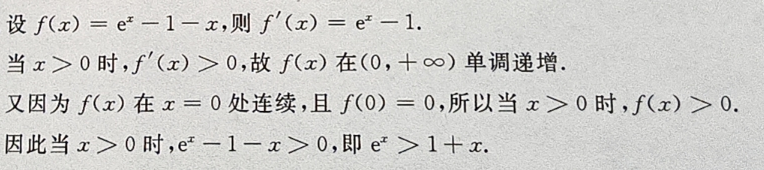单选题
1、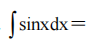
（）
答 案：D
解 析：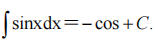
2、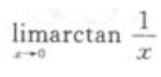
＝（）。
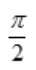
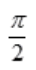
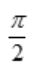
答 案：D
解 析：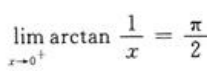
，
，所以
不存在。
3、对于微分方程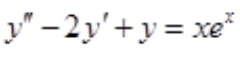
，利用待定系数法求其特解y*时，下列特解设法正确的是（）。
答 案：D
解 析：特征方程为r2－2r＋1＝0，特征根为r＝1（二重根），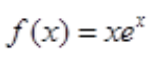
，a＝1为特征根，原方程特解为
。
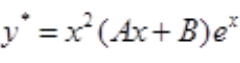主观题
1、设z＝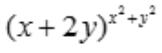
，求
。
答 案：解：令u＝x＋2y，v＝x2＋y2，根据多元函数的复合函数求导法则得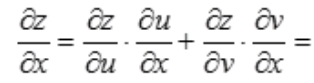
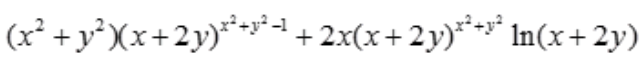
2、求微分方程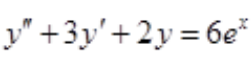
的通解．
答 案：解：原方程对应的齐次方程为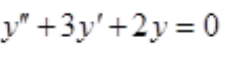
。特征方程为，r2＋3r＋2＝0，特征值为r1＝-2，r2＝-1。齐次方程的通解为y＝C1e-2x＋C2e-x。
设特解为y*＝Aex，代入原方程有6A＝6，得A＝1。
所以原方程的通解为y＝C1e-2x＋C2e-X＋ex（C1，C2为任意常数）。
3、用围墙围成216m2的一块矩形场地，正中间用一堵墙将其隔成左右两块，此场地长和宽各为多少时建筑材料最省?
答 案：解：设宽为xm，则长为
m，围墙总长为
,
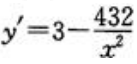，令y'＝0，得x＝±12，x＝12不合题意舍去。所以x＝12m是唯一驻点，而
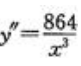，故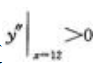
所以x＝12m时y最小，即长为18m，宽为12m时建筑材料最省。
填空题
1、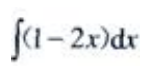
＝（）。
答 案：x-x2+C
解 析：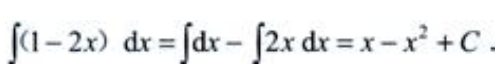
2、极限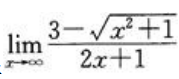
＝（）。
答 案：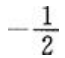
解 析：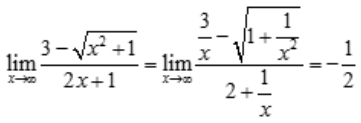
。
3、幂级数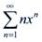
的收敛半径R＝（）。
答 案：1
解 析：对于级数
，
，
。
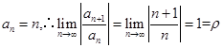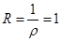简答题
1、证明：当x>0时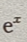
>1+x.
答 案：
