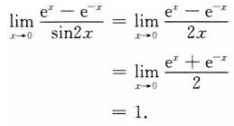单选题
1、在空间直角坐标系中,方程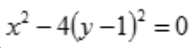 表示()。
表示()。
答 案:A
解 析:由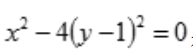 得
得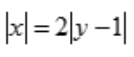 ,故为两个平面。
,故为两个平面。
2、若幂级数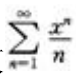 的收敛区间是[1,1),则级数
的收敛区间是[1,1),则级数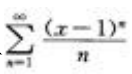 的收敛区间是()。
的收敛区间是()。
答 案:D
解 析:因为幂级数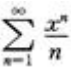 的收敛区间是[-1,1),则级数
的收敛区间是[-1,1),则级数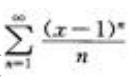 的收敛区间为
的收敛区间为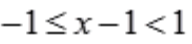 ,即
,即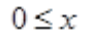 <2。
<2。
3、当x→0时,与3x2+2x3等价的无穷小量是()。
答 案:B
解 析:由于当x→0时,3x2为x的二阶无穷小量,2x3为x的三阶无穷小量,因此3x2+2x3为x的二阶无穷小量,即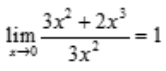 。
。
主观题
1、求y'+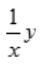 =1的通解.
=1的通解.
答 案:解:
2、求微分方程 的通解.
的通解.
答 案:解:对应齐次微分方程的特征方程为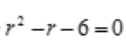 ,解得r1=3,r2=-2.所以齐次通解为
,解得r1=3,r2=-2.所以齐次通解为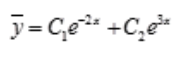 。设方程的特解设为y*=(Ax+B)ex,代入原微分方程可解得,A=
。设方程的特解设为y*=(Ax+B)ex,代入原微分方程可解得,A=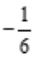 ,B=
,B=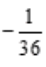 .即非齐次微分方程特解为
.即非齐次微分方程特解为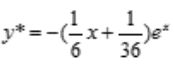 。所以微分方程
。所以微分方程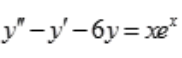 的通解为
的通解为 。
。
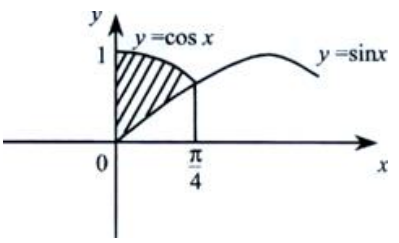
3、求曲线y=sinx、y=cosx、直线x=0在第一象限所围图形的面积A及该图形绕x轴旋转一周所得旋转体的体积Vx。
答 案:解:由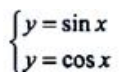 ,解得两曲线交点的x坐标为
,解得两曲线交点的x坐标为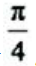 。
。
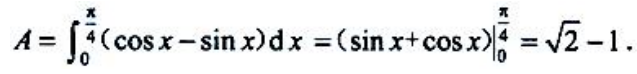

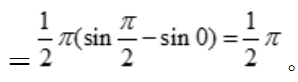
填空题
1、直线 的标准式方程为()。
的标准式方程为()。
答 案:
解 析:取z=0,可得直线上一点(-5,-8,0)直线的方向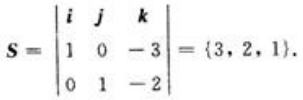 所以直线方程为:
所以直线方程为:
2、设y=f(x)可导,点x0=2为f(x)的极小值点,且f(2)=3,则曲线y=f(x)在点(2,3)处的切线方程为()。
答 案:y=3
解 析:由于y=f(x)可导,且点x0=2为f(x)的极小值点,由极值的必要条件可得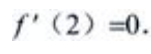 又f(2)=3,可知曲线过点(2,3)的切线方程为
又f(2)=3,可知曲线过点(2,3)的切线方程为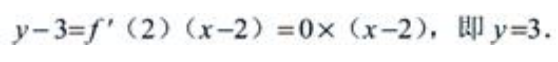
3、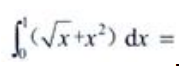 ()。
()。
答 案:1
解 析: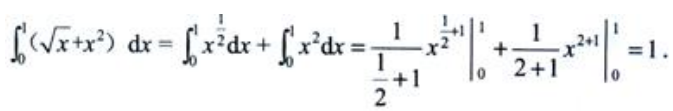
简答题
1、计算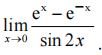
答 案: