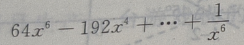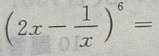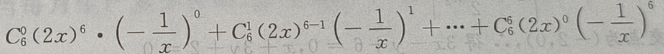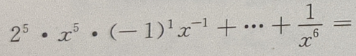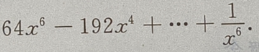单选题
1、已知集合M =(2,3,5,a),N =(1,3,4,b),若M∩N=(1,2,3),则a,b的值为
答 案:C
解 析:M∩N={2,3,5,a} ∩{1,3,4,6} ={1,2,3} 又因为M中无“1”元素,而有“a”元素,只有a=1 而N中无“2”元素,而有“b元素”,只有b=2
2、已知偶函数y=f(x),在区间[a,b](0 答 案:B 解 析:由偶函数的性质:偶函数在[a,b]和[-b,-a]上有相反的单调性,可知,y=f(x)在区间[a,b](0 3、若 答 案:B 解 析:首先做出单位圆,然后根据问题的约束条件,利用三角函数线找出满足条件的a角取值范围 4、设 答 案:D 解 析:本题主要考查的知识点为三角函数的运算.当 主观题 1、记△ABC的内角A,B,C的对边分别为a,b,c,已知B=60°,b2=ac,求A。
答 案:由余弦定理b2=a2+c2-2accosB,可得ac=a2+c2-ac,即a2+c2-2ac=(a-c)2=0,解得a=c。
又因为B=60°,故△ABC为等边三角形,所以A=60° 2、建筑一个容积为8000 答 案: 3、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。
(I)求C的方程;
(Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB 答 案:(I)由题意,该抛物线的焦点到准线的距离为 4、在△ABC中,B=120°,BC=4,△ABC的面积为 答 案:由△ABC的面积为 填空题 1、过点(2,0)作圆x2+y2=1的切线,切点的横坐标为()。 答 案: 解 析:本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有 2、 答 案: 解 析: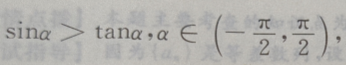 则
则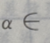 ()
()

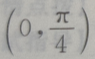
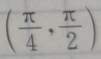
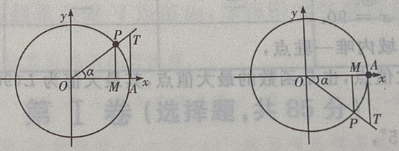
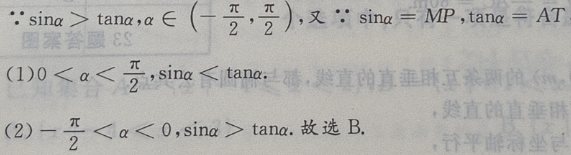
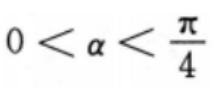 ,则
,则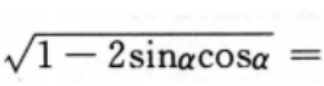 ()。
()。 时,
时,
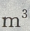 ,深为6m的长方体蓄水池,池壁每
,深为6m的长方体蓄水池,池壁每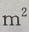 的造价为15元,池底每
的造价为15元,池底每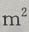 的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
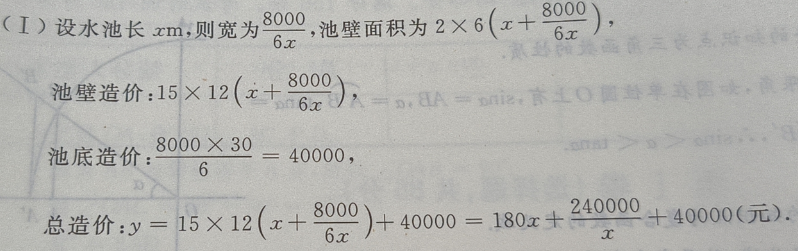

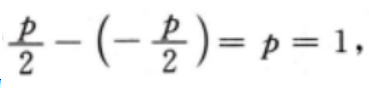 所以抛物线C的方程为
所以抛物线C的方程为 (Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得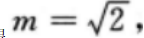 因此A点坐标为
因此A点坐标为 设B点坐标为
设B点坐标为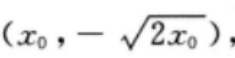 则
则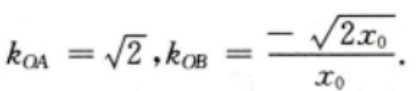 因为
因为 则有
则有 即
即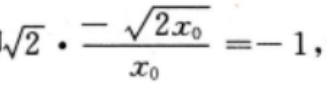 解得x0=4
所以B点的坐标为
解得x0=4
所以B点的坐标为
 ,求AC.
,求AC. 得
得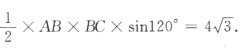 所以AB =4.因此
所以AB =4.因此 所以
所以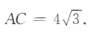
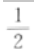
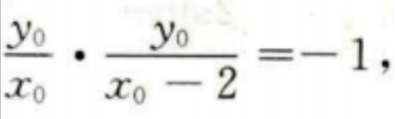 即
即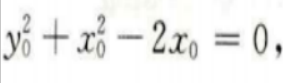
 所以
所以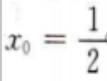 故切点横坐标为
故切点横坐标为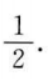
 的展开式是()
的展开式是()