单选题
1、若向量a=（1，-1），b=（1，x），且|a+b|=2，则x=（）。
答 案：C
解 析：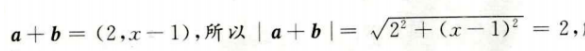
解得x=1 本题主要考查的知识点为向量的加法和模。
2、设集合S={(x,y)|xy>0},T={(x,y)|x>0,且y>0}，则
答 案：A
解 析：由已知条件可知集合S表示的是第第一,三象限的点集,集合T表示的是第一象限内点的集合,所以
所以有S∪T=S，S∩T=T，所以选择A。
3、若x 答 案：D 解 析：本题主要考查的知识点为不等式的性质。 因为 4、已知 答 案：D 解 析： 主观题 1、设函数 答 案：(I）因为 2、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)
答 案：如图 3、在△ABC中,已知三边 a、b、c 成等差数列,且最大角∠A是最小角的2倍, a: b :c.
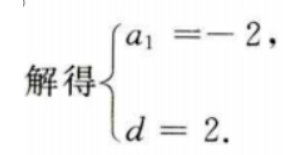
答 案： 4、已知等差数列{an}中，a1+a3+a5=6，a2+a4+a6=12，求{an}的首项与公差.
答 案：因为{an}为等差数列，则 填空题 1、过点（2，0）作圆x2+y2=1的切线，切点的横坐标为（）。 答 案： 解 析：本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有 2、 答 案：3 解 析：
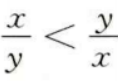
，则sin2α=（）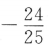
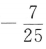
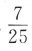
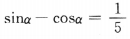两边平方得
，故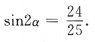
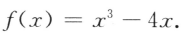
(I）求f'(2)；
(II）求f(x）在区间[一1,2]的最大值与最小值．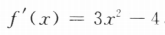
，所以f'(2)=3×22-4=8.(II）因为x＜-1，f(-1)=3.
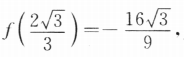f(2)=0.
所以f(x）在区间[一1,2]的最大值为3，最小值为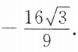
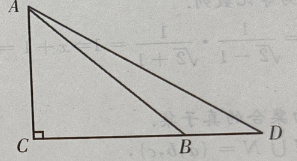
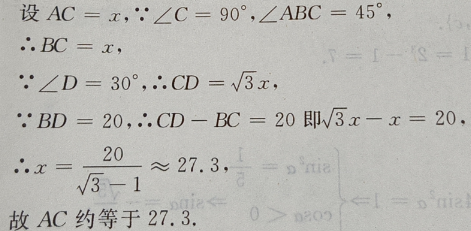
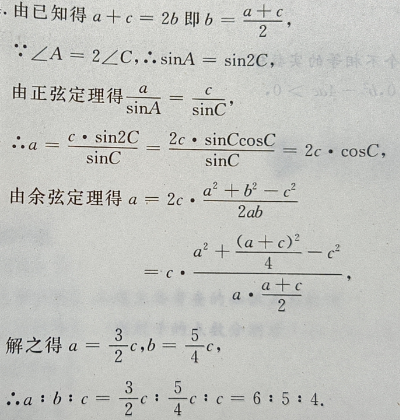
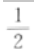
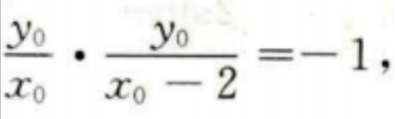即
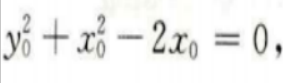
所以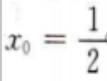
故切点横坐标为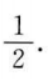
（）
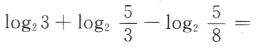