单选题
1、若tanα=3，则
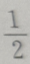
答 案：A
解 析：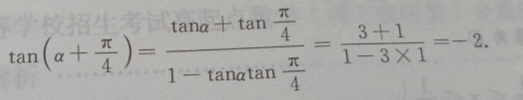
2、设集合M＝{0，1，2，3，4}，N＝{1，2，3}，T＝{2，4，6}，则集合（M∩T）∪N＝（）。
答 案：B
解 析：M∩T＝（2，4），则集合（M∩T）∪N＝{1，2，3，4}。答案为B。
3、函数y=sinx+cosx（x∈R）的最小正周期为（）。
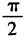
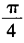
答 案：A
解 析：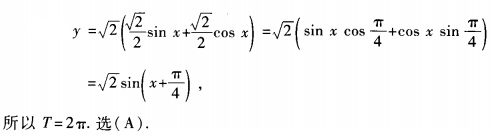
4、
展开式中,末3项的系数(a,x 均未知) 之和为()
答 案：C
解 析：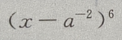
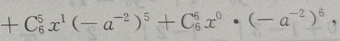末三项数之和为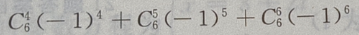
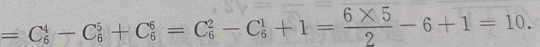
主观题
1、已知am=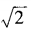
，an=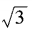
，求a3n-4m的值。
答 案：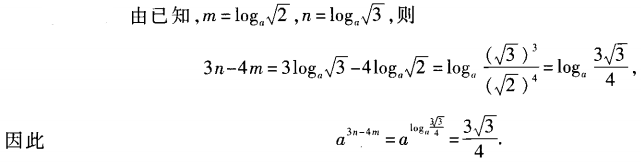
2、已知a,b,c成等差数列，a,b,c+1成等比数列．若b=6，求a和c．
答 案：由已知得
解得
3、已知直线l的斜率为1，l过抛物线C：
的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.
答 案：(I）C的焦点为
，准线为
由题意得l的方程为
因此l与C的准线的交点坐标为
(II）由
，得
设A（x1,y1），B（x2,y2），则
因此
4、化简： （1）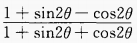
（2）
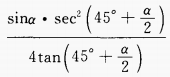
答 案：（1）
（2）
填空题
1、lg(tan43°tan45°tan47°)=（）
答 案：0
解 析：lg(tan43°tan45°tan47°)=lg(tan43°tan45°cot43°)=lgtan45°=lg1=0
2、y=ax2-bx+c的导数y'|x=1=______。
答 案：2a-b
