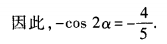单选题
1、已知二次函数y=x2+ax+1在区间[1，+∞)上为递增函数，则实数a的取值范围是（ ）
答 案：A
解 析：先配方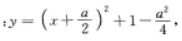
可知其图像的对称轴为
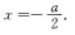画出其图像的草图，即可得出
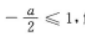解得a≥-2
考点 本题主要考查二次函数的单调区间以及配方法和数形结合的思想在解题中的应用．
2、由数字1、2、3、4组成没有重复数字的两位数共有（）。
答 案：B
3、若A（-3，5），B（-5，-3），则线段AB中点的坐标为（）。
答 案：B
4、设集合M={x||x-2||＜2}，N={0,1,2,3,4}，则M∩N=（）
答 案：C
解 析：解得M={x||x-2||＜2}={x|-2＜x-2＜2}={x|0＜x＜4}，故M∩N={1,2,3}.
主观题
1、设椭圆的中心是坐标原点,长轴在x轴上,离心率
已知点P
到圆上的点的最远距离是
求椭圆的方程
答 案：由题意，设椭圆方程为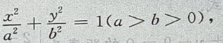
由
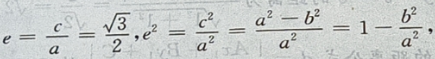
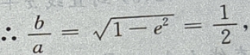设P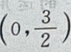
点到椭圆上任一点的距离为 d,
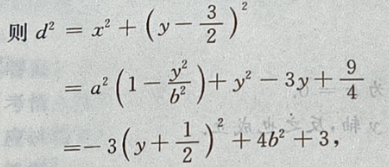
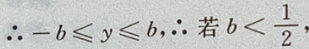则在y=-b时，
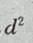最大，即d也最大。
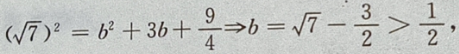
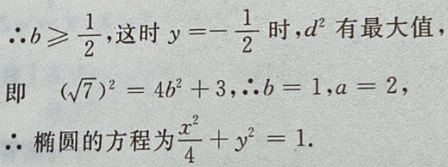
2、已知等差数列{an}中，a1+a3+a5=6，a2+a4+a6=12，求{an}的首项与公差.
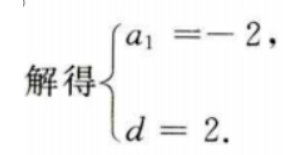
答 案：因为{an}为等差数列，则
3、已知F是椭圆
的右焦点，点M在抛物线y2=2px（p＞0）上O为坐标原点，且△MOF为正三角形．
(Ⅰ)求P的值； (Ⅱ)求抛物线的焦点坐标和准线方程．
答 案：(Ⅰ)由椭圆方程可知，椭圆的长半轴a=5，短半轴，则椭圆的半焦距
即椭圆的右焦点F的坐标为
(4.0).
如图,因为△MOF为正三角形,OF=4,过M作MN⊥OF于N点，
【考点指要】本题主要考查椭圆、抛物线的概念，要求考生掌握它们的标准方程和性质，会用它们解决有关的问题．
4、已知直线l的斜率为1，l过抛物线C：
的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．
答 案：(I）C的焦点为
，准线为
由题意得l的方程为
因此l与C的准线的交点坐标为
(II）由
得
设A（x1,y1）.B（x2,y2），则
因此
填空题
1、log2[log2（log381）]=______。
答 案：1
解 析：由于log381=log334=4，于是 原式=log2（log24）=log22=1。
2、已知点P（-3，1）为角α终边上一点，则cos（2α-π）的值等于______。
答 案：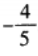
解 析：因为cos（2α-π）=cos（π-2α）=-cos2α。由已知，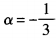
所以
