单选题
1、要得到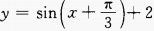 的图像,只需将y=sinx的图像().
的图像,只需将y=sinx的图像().
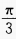 ,再向上平移2个单位
,再向上平移2个单位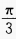 ,再向下平移2个单位
,再向下平移2个单位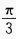 ,再向上平移2个单位
,再向上平移2个单位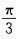 ,再向下平移2个单位
,再向下平移2个单位答 案:A
解 析: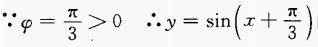 的图像是由y=sinx的图像向左平移
的图像是由y=sinx的图像向左平移 个单位,再向上平移2个单位而得到
个单位,再向上平移2个单位而得到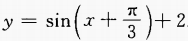
2、过直线3x+2y+1=0与2x-3y+5=0的交点,且垂直于直线L:6x-2y+5=0的直线方程是()。
答 案:B
解 析: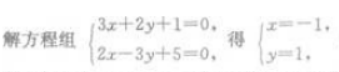 即两直线的交点坐标为(-1,1)
又直线L:6x-2y+5=0的斜率为3 ,则所求的直线方程为
即两直线的交点坐标为(-1,1)
又直线L:6x-2y+5=0的斜率为3 ,则所求的直线方程为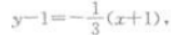 即x+3y-2=0.
即x+3y-2=0.
3、函数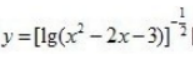 定义域为()。
定义域为()。
答 案:D
4、直线l1与l2:3x + 2y - 12 =0 的交点在x轴上,且l1⊥l2,则l1在y轴的截距是()。
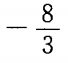
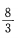
答 案:B
解 析:
主观题
1、设 分别讨论x→0及x→1时f(x)的极限是否存在?
分别讨论x→0及x→1时f(x)的极限是否存在?
答 案: ∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
2、求函数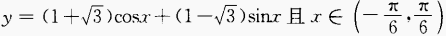 上的最大值以及取得这个最大值的x。
上的最大值以及取得这个最大值的x。
答 案:.1 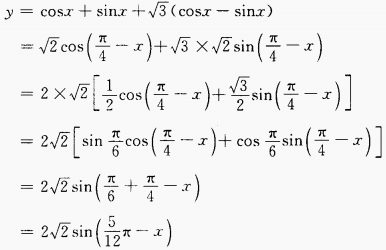
 函数取最大值,即y最大值=。
函数取最大值,即y最大值=。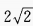
3、已知设△ABC的三边长为a、b、C,2sin2A=3(sin2B+sin2C)且cos2A+3cosA+3cos(B-C)=1,求证:a:b:c= :1:1。
:1:1。
答 案:因所证的是△ABC三边的比,所以可将题中角的关系式转化为边的关系式,需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin2A=3(sin2B+sin2C)…① 由正弦定理得,2a2=3(b2+c2)…②
∵cos2A+3cosA+3cos(B-C)=1
∴3[cosA+cos(B-C)]=1-cos2A.
∵A=180°-(B+C)
∴3[-cos(B+C)+cos(B-C)]=2sin2A.
由两角和与差的余弦公式得
6sinBsinB=2sin2A…③
由①③得,2sinBsinC=sin2B+sin2C.
sin2B-2sinBsinC+sin2C=0
(sinB-sinC)2=0
sinB= sinC.
由正弦定理得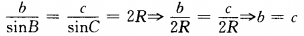
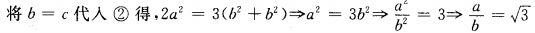
∴a:b=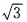 :1
:1
于是a:b:c=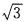 :1:1。
:1:1。
4、记△ABC的内角A,B,C的对边分别为a,b,c,已知B=60°,b2=ac,求A。
答 案:由余弦定理b2=a2+c2-2accosB,可得ac=a2+c2-ac,即a2+c2-2ac=(a-c)2=0,解得a=c。 又因为B=60°,故△ABC为等边三角形,所以A=60°
填空题
1、cos267.5°- 0.5=______。
答 案:
解 析:
2、椭圆的中心在原点,一个顶点和一个焦点分别是直线x+3y-6与两坐标轴的交点,则此椭圆的标准方程为()
答 案: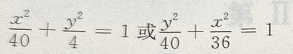
解 析:原直线方程可化为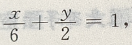 交点(6,0),(0,2). 当点(6,0)是椭圆一个焦点,点(0,2) 是椭圆一个顶点时,c=6,b=2,
交点(6,0),(0,2). 当点(6,0)是椭圆一个焦点,点(0,2) 是椭圆一个顶点时,c=6,b=2, 当点(0,2) 是椭圆一个焦点,(6,0) 是椭圆一个顶点时,c=2,b-6,
当点(0,2) 是椭圆一个焦点,(6,0) 是椭圆一个顶点时,c=2,b-6,