单选题
1、从1、2、3、4、5、6、7、8、9这九个数字中，随机取出一个数字，这个数字是奇数的概率是（）。
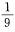
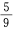
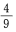
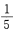
答 案：B
解 析：本题的试验是从1~9这九个数字中任取一个数字，显然选中其中任一个数字的可能 性都是相同的，属于等可能事件的概率，∵n=9，其中奇数个数m=5，∴其概率是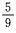
，故选B。
2、设函数f(x－2)＝x2－3x－2，则f(x)＝（）。
答 案：A
解 析：令x-2=t,得x=t+2代入原式,得f(t)=(t+2)2-3(t+2)-2=t2+t-4.即f(x)=x2+x-4.(答案为 A)
3、
展开式中,末3项的系数(a,x 均未知) 之和为()
答 案：C
解 析：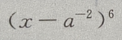
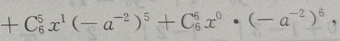末三项数之和为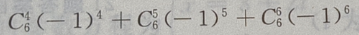
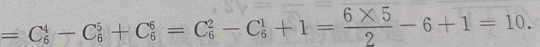
4、已知集合M =(2,3,5,a),N =(1,3,4,b),若M∩N=(1,2,3),则a,b的值为
答 案：C
解 析：M∩N={2,3,5,a} ∩{1,3,4,6} ={1,2,3} 又因为M中无“1”元素，而有“a”元素，只有a=1 而N中无“2”元素，而有“b元素”，只有b=2
主观题
1、求将抛物线y=x2-2x-3平移到顶点与坐标原点重合时的函数解析式。
答 案：
2、设A1A2A3A4A5A6为正六边形，如图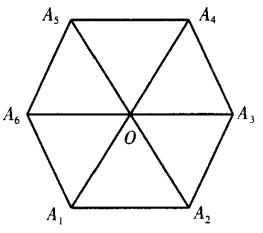
，O为它的中心。 （1）求证： 
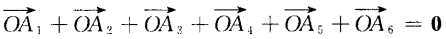（2）
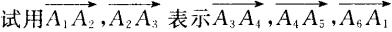
答 案：已知A1A2A3A4A5A6 为正六边形，即|A1A2|=|A3A4|=......|A6A1|.要证6个向量的和为0.只需证其中3个向量与另3个向量的长度相等、方向相反即可.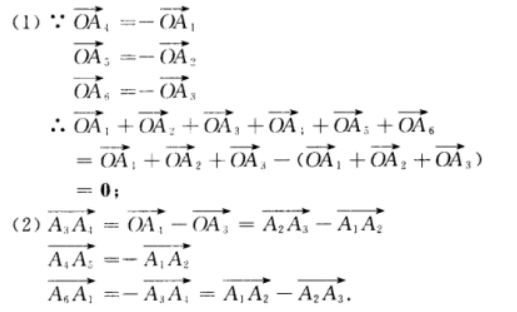
3、求下列函数的最大值、最小值和最小正周期： （1）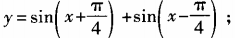
（2）y=6cosx+8sinx
答 案：
4、已知数列{an}中，a1=2，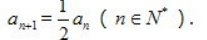
（Ⅰ）求数列{an}的通项公式;
（Ⅱ）求数列{an}前5项的和 S5
答 案：解：
填空题
1、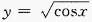
的定义域是______。
答 案：1
解 析：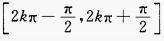
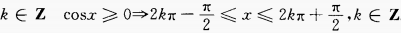
2、100件产品中有3件次品，每次抽取一件，有放回的抽取三次，恰有1件是次品的概率是______。
答 案：0.0847
解 析：由于三次抽取是独立的，每次抽取可看做是一次试验，每次试验只有两个可能结果：“正品”或“次品”，次品率为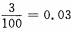
，因此二次独立且重复试验恰有1件次品率为
