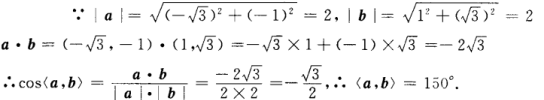单选题
1、一批产品共有5件,其中4件为正品,1件为次品,从中一次取出2件均为正品的概率为()。
答 案:A
解 析:本题主要考查的知识点为随机事件的概率
一次取出2件均为正品的概率为
2、在△ABC中,AB=4,BC=6,∠ABC=60°,则AC=()。
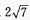
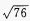
答 案:C
解 析:已知两边及夹角用余弦定理得 AC2=62+42-2×6×4cos60°=28
∴AC=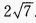
3、已知全集U=R,A={x|x≥1},B={x|-1
答 案:A
解 析:补集运算应明确知道是否包括端点.A在U中的补集是x<1, 


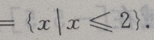
4、下列各式的值为零的是()。
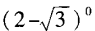
答 案:D
解 析:00和log11均没有意义,可排除(A)、(B),而(2-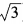 )0=1。故选D。
)0=1。故选D。
主观题
1、求将抛物线y=x2-2x-3平移到顶点与坐标原点重合时的函数解析式。
答 案:
2、求函数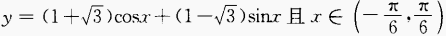 上的最大值以及取得这个最大值的x。
上的最大值以及取得这个最大值的x。
答 案:.1 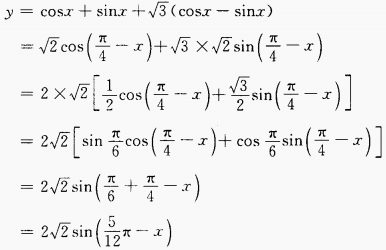
 函数取最大值,即y最大值=。
函数取最大值,即y最大值=。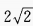
3、某工厂每月生产x台游戏机的收入为R(x)= +130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
+130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
答 案:利润 =收入-成本, L(x)=R(x)-C(x)= +130x-206-(50x+100)=
+130x-206-(50x+100)=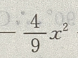 +80x-306
法一:用二次函数
+80x-306
法一:用二次函数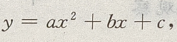 当a<0时有最大值
当a<0时有最大值
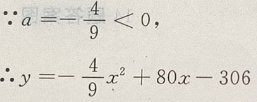 是开口向下的抛物线,有最大值
是开口向下的抛物线,有最大值
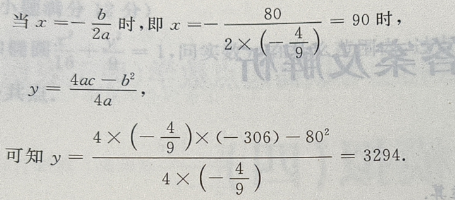 法二:用导数来求解
法二:用导数来求解
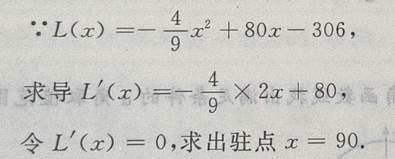 因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
4、在△ABC中,B=120°,BC=4,△ABC的面积为 ,求AC.
,求AC.
答 案:由△ABC的面积为 得
得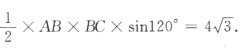 所以AB =4.因此
所以AB =4.因此 所以
所以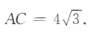
填空题
1、函数y=2cosx-cos2x(x∈R)的最大值为______。
答 案: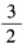
解 析: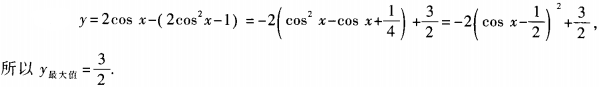
2、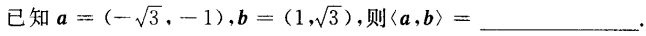
答 案:;150°
解 析: