单选题
1、已知空间向量i,j,k为两两垂直的单位向量,向量a=2i+3j+mk,若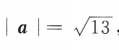 ,则m=()
,则m=()
答 案:C
解 析:由题可知向量a=(2,3,m),故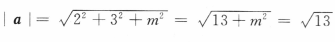 ,解得m=0.
,解得m=0.
2、在△ABC中,已知a=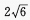 ,b=
,b=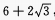 ,c=
,c=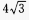 ,则()。
,则()。
答 案:C
解 析:由已知a= 3、设α是第一象限角 答 案:C 解 析:本题主要考查的知识点为三角函数的二倍角公式。 α在第一象限,则 4、函数f(x)=x3-6x2+9x-3的单调区间为()。 答 案:C 解 析:y=x3-6x2+9x-3则y’=3x2+12x+9 令y’=0,x2-4x+3=0 主观题 1、已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。 答 案:由已知,得 2、某气象预报站天气预报的准确率为80%,计算(1)5次预报中恰有4次准确的概率; (2)5次中至少有次准确的概率.(计算结果保留两个有效数字).
答 案: 把每次预报看做一次试验,“预报结果准确”看成事件P(A)=0.8,本题就相当于在5次独立重复试验中求A恰好发生4次(或至少4次)的概率,此题属于独立重复试验,由公式 3、设 答 案: 4、(1)已知tanα= 答 案:(1) 填空题 1、在△ABC中,a=2,b= 答 案: 解 析: 2、化简sin(x+y)-2cosxsiny=______.
答 案:sin(x-y) 解 析:原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin(x-y)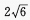 ,b=
,b=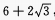 ,c=
,c=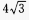 可知a
可知a ,则sin2α=()。
,则sin2α=()。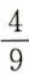
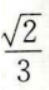
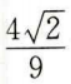
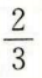
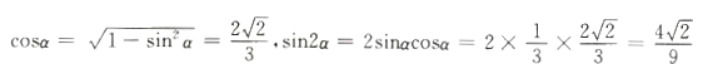
 (x-1)(x-3)=0解得,x1=1,x2=3 四个答案中,只有C具有1、3两个极值点,其余3个没有,故应选C。
(x-1)(x-3)=0解得,x1=1,x2=3 四个答案中,只有C具有1、3两个极值点,其余3个没有,故应选C。
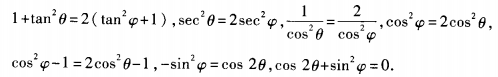
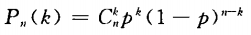 来求解。 (1)n=5;p=0.8;k=4
来求解。 (1)n=5;p=0.8;k=4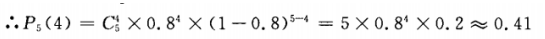 即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即
即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即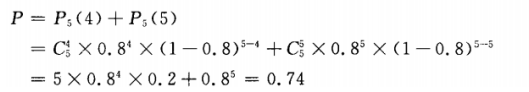 即至少有4次准确的概率为0.74。
即至少有4次准确的概率为0.74。
 分别讨论x→0及x→1时f(x)的极限是否存在?
分别讨论x→0及x→1时f(x)的极限是否存在? ∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在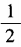 ,求cot2α的值; (2)已知tan2α=1,求tanα的值。
,求cot2α的值; (2)已知tan2α=1,求tanα的值。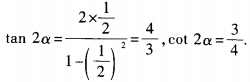 (2)由已知,得
(2)由已知,得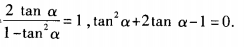 解关于tanα的一元二次方程,得tanα=
解关于tanα的一元二次方程,得tanα=
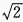 ,∠B=
,∠B=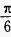 ,则∠A=______。
,则∠A=______。