单选题
1、i为虚数单位,则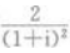 的值为()。
的值为()。
答 案:D
解 析: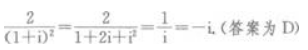
2、函数y=x2—2x+6在区间(-∞,1)、(1,+∞)分别()。
答 案:B
解 析:方法一:用配方法把y=x2-2x+6配成完全平方式。 y=x2-2x+6=(x-1)2+5,开口向上的抛物线顶点坐标为(1,5),可得出单调区间。 方法二:用导数判定。y’=2x-2=2(x-1)
当x<1时,y’<0,单调减少;当x>1时,y>0,单调增加。
3、函数y=sinx+cosx(x∈R)的最小正周期为()。
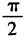
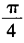
答 案:A
解 析: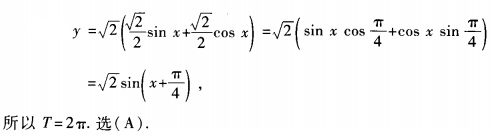
4、顶点在坐标原点,准线方程为y=4的抛物线方程式()。
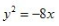
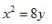
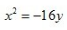
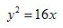
答 案:C
主观题
1、计算。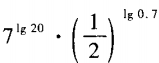
答 案: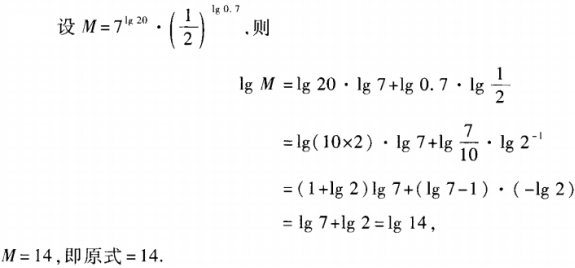
2、已知x+x-1=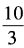 ,求x2+x-2的值。
,求x2+x-2的值。
答 案:由已知,得

3、已知数列 的前n项和
的前n项和 求证:
求证: 是等差数列,并求公差和首项。
是等差数列,并求公差和首项。
答 案:

4、在△ABC中,B=120°,BC=4,△ABC的面积为 ,求AC.
,求AC.
答 案:由△ABC的面积为 得
得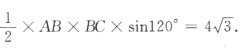 所以AB =4.因此
所以AB =4.因此 所以
所以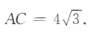
填空题
1、已知函数y=a2+bx+c的图像是以(6,-12)为顶点的抛物线,并且与x轴的一个交点坐标是(8,0),则a=(),b=(),c=()
答 案: 3;-36;96
解 析:根据顶点坐标是(6,-12),设y=a(x-6)2-12(8,0)代入得:0=a*(8-6)2-12得到a=3
即y=3(x-6)2-12=3x2-36x+96
故a=3,b=-36,c=96
2、已知角α的终边过点P(-8m,-6cos60°)且cosα=-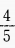 ,则m______。
,则m______。
答 案: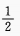
解 析:∵P(-8m,-3)且cosα= ∴P点在第三象限
∴m>0∵y=-3,r=5∴x=-8m=-4
∴P点在第三象限
∴m>0∵y=-3,r=5∴x=-8m=-4