单选题
1、下列函数中,为增函数的是()。


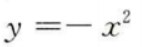
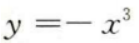
答 案:A
解 析:本题主要考查的知识点为函数的单调性。 对于y=x3,y′=3x2≥0,故y=x3为增函数。
2、在∆ABC中,∠ABC=600,AB=4,BC=6,则AC=()。
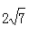
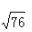
答 案:C
3、已知圆的半径为R,弧长为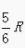 的弧所对的圆心角等于()。
的弧所对的圆心角等于()。
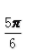
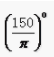
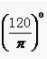
答 案:B
4、用列举法表示集合{(x,y)|x+2y=7且x,y为正整数},结果是()。
答 案:B
主观题
1、设函数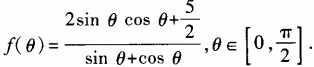 (1)求
(1)求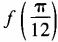 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
2、已知am=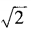 ,an=
,an=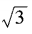 ,求a3n-4m的值。
,求a3n-4m的值。
答 案: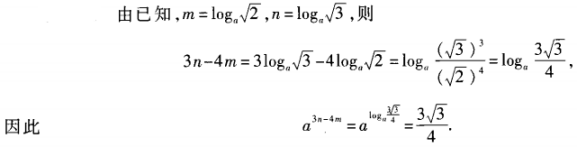
3、已知F是椭圆 的右焦点,点M在抛物线y2=2px(p>0)上O为坐标原点,且△MOF为正三角形.
(Ⅰ)求P的值; (Ⅱ)求抛物线的焦点坐标和准线方程.
的右焦点,点M在抛物线y2=2px(p>0)上O为坐标原点,且△MOF为正三角形.
(Ⅰ)求P的值; (Ⅱ)求抛物线的焦点坐标和准线方程.
答 案:(Ⅰ)由椭圆方程可知,椭圆的长半轴a=5,短半轴,则椭圆的半焦距 即椭圆的右焦点F的坐标为
(4.0).
即椭圆的右焦点F的坐标为
(4.0). 如图,因为△MOF为正三角形,OF=4,过M作MN⊥OF于N点,
如图,因为△MOF为正三角形,OF=4,过M作MN⊥OF于N点, 【考点指要】本题主要考查椭圆、抛物线的概念,要求考生掌握它们的标准方程和性质,会用它们解决有关的问题.
【考点指要】本题主要考查椭圆、抛物线的概念,要求考生掌握它们的标准方程和性质,会用它们解决有关的问题.
4、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35° 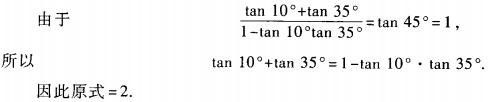
填空题
1、不等式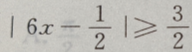 的解集是()
的解集是()
答 案: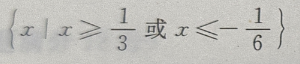
解 析: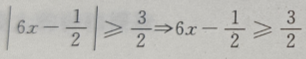 或
或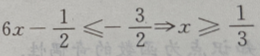 或
或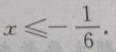
2、平面内有10个点,任何三点都不在同一直线上,问能连成______条不同的直线。
答 案:45