单选题
1、中心在坐标原点,一个焦点的坐标是(-3,0),一条渐近线方程式 的双曲线方程是()。
的双曲线方程是()。
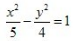
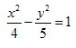
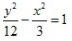
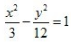
答 案:B
2、在△ABC中,若b=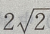 ,c=
,c=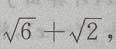
 则a等于()
则a等于()
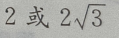
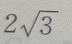
答 案:B
解 析:此题是已知两边和其中一边的对角,解三角形时,会出现一解、两解、无解的情况,要注意这一点.用余弦定理 可得
可得

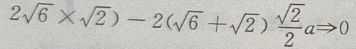
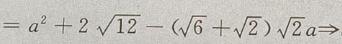
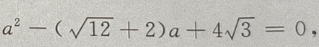 解出
解出


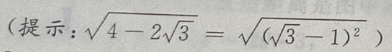
3、已知a,b为任意正实数,则下列等式中恒成立的是()。
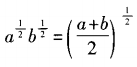
答 案:D
解 析:由于a,b为任意正实数,不妨取a=1,b=2。在A项中,12≠21;B项中,21+2≠21+22;C项中,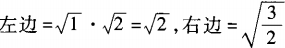 ,而
,而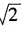 ≠
≠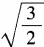 。故选D。
。故选D。
4、三个数0,30.7,log30.7的大小关系是()。
答 案:B
主观题
1、化简: (1)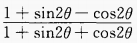
(2)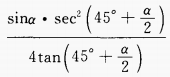
答 案:(1) (2)
(2)
2、计算 (1)tan5°+ cot5°- 2sec80°
(2)tan15°+cot15
(3)sin15°sin75°
答 案:(1)化切割为弦进行运算。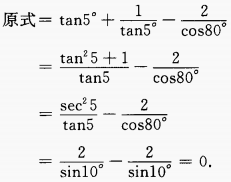 (2)
(2) 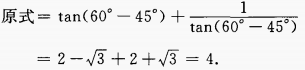 (3)
(3) 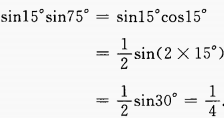
3、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 ,得
,得 设A(x1,y1),B(x2,y2),则
设A(x1,y1),B(x2,y2),则 因此
因此
4、已知设△ABC的三边长为a、b、C,2sin2A=3(sin2B+sin2C)且cos2A+3cosA+3cos(B-C)=1,求证:a:b:c= :1:1。
:1:1。
答 案:因所证的是△ABC三边的比,所以可将题中角的关系式转化为边的关系式,需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin2A=3(sin2B+sin2C)…① 由正弦定理得,2a2=3(b2+c2)…②
∵cos2A+3cosA+3cos(B-C)=1
∴3[cosA+cos(B-C)]=1-cos2A.
∵A=180°-(B+C)
∴3[-cos(B+C)+cos(B-C)]=2sin2A.
由两角和与差的余弦公式得
6sinBsinB=2sin2A…③
由①③得,2sinBsinC=sin2B+sin2C.
sin2B-2sinBsinC+sin2C=0
(sinB-sinC)2=0
sinB= sinC.
由正弦定理得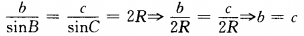
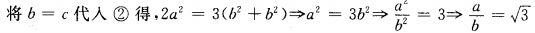
∴a:b=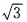 :1
:1
于是a:b:c=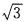 :1:1。
:1:1。
填空题
1、函数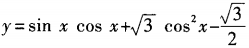 (x∈R)的最小值为______。
(x∈R)的最小值为______。
答 案:-1
解 析: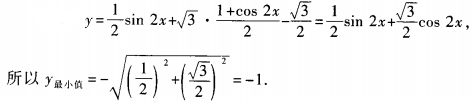
2、sin210°+sin220°+sin240°+sin250°+sin270°+sin280=______。
答 案:3
解 析:由互为余角的余函数值相等得 原式=(sin210°+cos210°)+(sin220°+cos220°)+(sin240+cos240)=1+1+1=3