单选题
1、下列函数中，为偶函数的是（）。
答 案：D
2、已知sinα=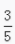
且
，则sin（α+
）的值等于（）。
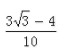
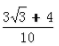
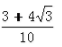
答 案：C
3、函数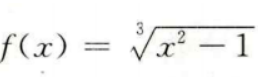
的定义域为（）。
答 案：A
解 析：本题主要考查的知识点为函数的定义域。 对于
奇次根号下无要求，故函数的定义域为R。
4、函数f(x)=
当x∈[-2,+∞)时是增函数，当x∈(-∞,-2]时是减函数，则f(1)=()
答 案：B
解 析：由题意知抛物线的对称轴为x=-2，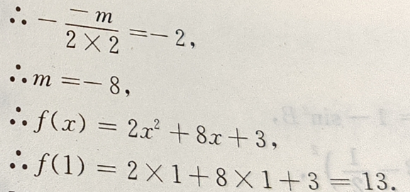 
主观题
1、设函数f(x)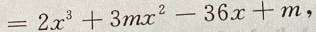
且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
答 案：(Ⅰ)由已知得f'=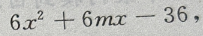
又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=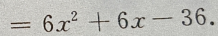
令f'(x)=0，解得
当x<-3时，f'(x)>0;
当-3
2、教室里有50人在开会，其中学生35人，家长12人，老师3人，现校长在门外听到有人在发言，那么发言人是老师或学生的概率为多少？
答 案：此题属于互斥事件，发言人是老师的概率为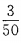
，是学生的概率为
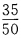，故所求概率为。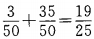
3、设函数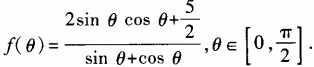
（1）求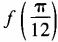
；（2）求函数f（θ）最小值。
答 案：
4、已知tan2θ=2tan2ψ+1，求cos2θ+sin2ψ的值。
答 案：由已知，得 
填空题
1、“a=0，且b=0”是“a2+b2=0的”______。
答 案：充要条件
2、已知5a=2，25b=9，则52a-b的值等于______。
答 案：
解 析：由25b=9，得52b=9，5b=3。又5a=2，则 
