单选题
1、设0<x<1,则()。
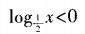
答 案:A
解 析:函数y=2x在区间(-∞,+∞)内为增函数,则2x>20=1,且2x<21=2,选A。
2、袋中有6个球,其中4个红球,2个白球,从中随机取出2个球,则这2个球都为红球的概率为()
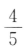
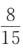
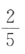

答 案:C
解 析:两个球都是红球的概率为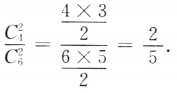
3、在∆ABC中,∠ABC=600,AB=4,BC=6,则AC=()。
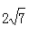
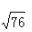
答 案:C
4、已知函数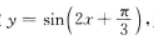 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
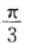 得到的
得到的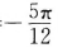 成轴对称图形
成轴对称图形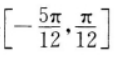
答 案:C
解 析:显然它不是奇函数,不能认为含有“sin”符号的函数就是奇函数,故A项错误.图象的平移要看函数式中的自变量z的变化情况.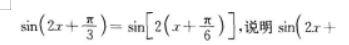
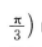 的图象是把 sin2x 的图象向左平
的图象是把 sin2x 的图象向左平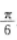 。一般说来,sin(ωx+y)的图象是将sinωx 的图象沿x轴正方向平移了
。一般说来,sin(ωx+y)的图象是将sinωx 的图象沿x轴正方向平移了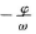 而得到的,故B项错误,过函数y=sinx的每一个最大值点或最小值点(即使sinx=1或-1的点)作x轴的垂线,都是其函数图象的对称轴
而得到的,故B项错误,过函数y=sinx的每一个最大值点或最小值点(即使sinx=1或-1的点)作x轴的垂线,都是其函数图象的对称轴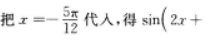
 【考点指要】本题考查了三角函数的奇偶性、单调性以及图象的平移与对称轴,对三角函数的性质进行了较全面的考查.
【考点指要】本题考查了三角函数的奇偶性、单调性以及图象的平移与对称轴,对三角函数的性质进行了较全面的考查.
主观题
1、在△ABC中,已知AB=2,BC=1,CA=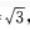 点D,E,F分别在AB,BC,CA边上,△DEF为正三角形,记∠FEC为α,如果sinα=
点D,E,F分别在AB,BC,CA边上,△DEF为正三角形,记∠FEC为α,如果sinα=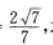 求△DEF的边长。
求△DEF的边长。
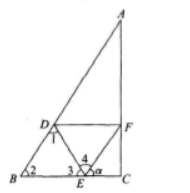
答 案:解析:由AB=2,BC=1,CA=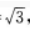 得BC2=CA2=AB2,因此∠C=90°,如图所示。
因为sinA=
得BC2=CA2=AB2,因此∠C=90°,如图所示。
因为sinA= 所以∠A=30°,于是∠b=60°。
设正△DEF边长为l,已知AB=2,sinα=
所以∠A=30°,于是∠b=60°。
设正△DEF边长为l,已知AB=2,sinα=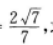 由此EC=lcosα
由此EC=lcosα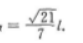 有图知,∠1+∠2+∠3=180°(三角形内角和);
∠3+∠4+α=180°,因为∠2-∠4=60°,所以∠1=α。
有图知,∠1+∠2+∠3=180°(三角形内角和);
∠3+∠4+α=180°,因为∠2-∠4=60°,所以∠1=α。
 【考点指要】本题主要考查三角函数的概念、同角三角函数的关系及正弦定理,这些均是考试大纲要求掌握的重要概念,并要求能达到灵活应用的程度,此类题是在成人高考中出现频率较高的题型,
【考点指要】本题主要考查三角函数的概念、同角三角函数的关系及正弦定理,这些均是考试大纲要求掌握的重要概念,并要求能达到灵活应用的程度,此类题是在成人高考中出现频率较高的题型,
2、已知三角形的三边边长组成公差为1的等差数列,且最大角是最小角的二倍,求三边之长。
答 案:三角形的三边边长分别为4,5,6。
3、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.
的焦点,且与C交于A,B两点.
(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 得
得 设A(x1,y1).B(x2,y2),则
设A(x1,y1).B(x2,y2),则 因此
因此
4、求下列函数的最大值、最小值和最小正周期: (1)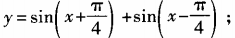 2)y=6cosx+8sinx
2)y=6cosx+8sinx
答 案: 所以函数的最大值是
所以函数的最大值是 最小值是
最小值是 最小正周期为2π,
(2)要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式,需使cosx与sinx的系数平方和为1,为此,将已知函数化为
最小正周期为2π,
(2)要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式,需使cosx与sinx的系数平方和为1,为此,将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π
因此,函数的最大值是10,最小值是-10,最小正周期为2π
填空题
1、在等比数列中,a1=3,an=96,Sn=189,则公比q=______,项数n=_______。
答 案:q=2,n=6
解 析:解法一:An=A1×q^(n-1)=3q^(n-1)=96q^(n-1)=32S(n-1)=Sn-An=189-96=93
S(n-1)=A1×(1-q^(n-1))/(1-q)
=3(1-32)/(1-q)=93
q=2
2^(n-1)=32
n=6
解法二:

2、不等式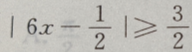 的解集是()
的解集是()
答 案: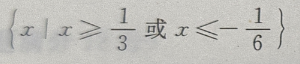
解 析: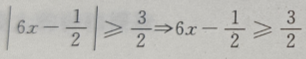 或
或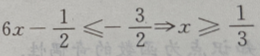 或
或