单选题
1、已知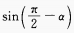 =
=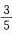 ,则
,则 =()。
=()。
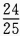
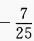
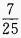
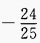
答 案:C
解 析: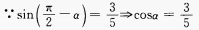
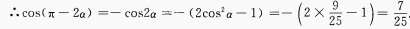
2、设F1,F2分别是椭圆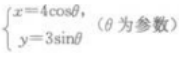 焦点,并且B1是该椭圆短轴的一个端点,则△F1F2B1的面积等于()。
焦点,并且B1是该椭圆短轴的一个端点,则△F1F2B1的面积等于()。
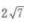
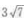
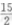
答 案:B
解 析:消去参数,将参数方程化为普通方程,F1F2分别是椭圆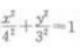 的焦点。
的焦点。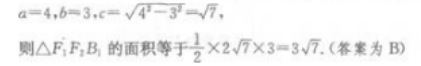
3、对满足a>b的任意两个非零实数,下列不等式成立的是()
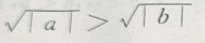
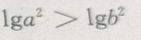

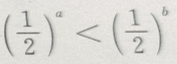
答 案:D
解 析:A错误,例如-2>4,而 B错误,例如:-10>100,而
B错误,例如:-10>100,而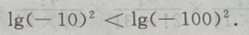 C错误,例如:-1>-2,而
C错误,例如:-1>-2,而
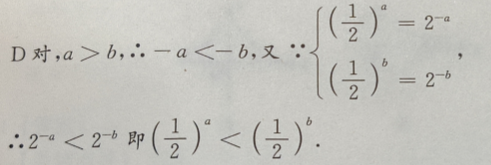
4、设函数f(x)=logax,且f(4)=2,则下列各式成立的是()。
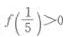
答 案:D
解 析:由f(4)-loga4=2,得a2=4,又a>0,故a=2,对于函数f(x)=logax,根据对数函数的性质有f(5)>f(3)成立.(答案为 D)
主观题
1、(1)已知tanα=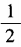 ,求cot2α的值; (2)已知tan2α=1,求tanα的值。
,求cot2α的值; (2)已知tan2α=1,求tanα的值。
答 案:(1)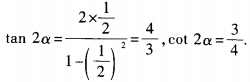 (2)由已知,得
(2)由已知,得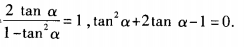 解关于tanα的一元二次方程,得tanα=
解关于tanα的一元二次方程,得tanα=
2、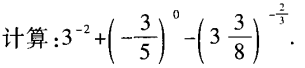
答 案: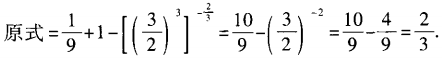
3、cos20°cos40°cos80°的值。
答 案:
4、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得 AB=120m,求河的宽
AB=120m,求河的宽

答 案:如图,  ∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD= =60m,
即河宽为60m
=60m,
即河宽为60m
填空题
1、过点(2,0)作圆x2+y2=1的切线,切点的横坐标为()。
答 案: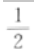
解 析:本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有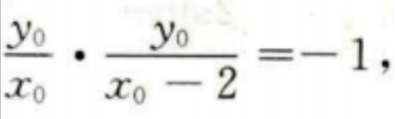 即
即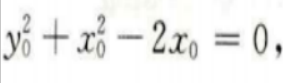
 所以
所以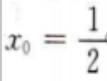 故切点横坐标为
故切点横坐标为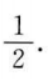
2、ABCD是正方形,E是AB的中点,如将△DAE和△CBE分别沿虚线DE、CE折起,使AE与BE重合如图 ,设A与B重合后的点为P,则面PCD与面ECD所成的二面角为______度,PE与面ECD成______度。
,设A与B重合后的点为P,则面PCD与面ECD所成的二面角为______度,PE与面ECD成______度。
答 案:二面角为30°,PE与面ECS成60角°
解 析:(1)求面PCD与面ECD所成的二面角为多少度,就是要求出由平面PCD与平面ECD所组成的二面角的平面角,其中画出二面角的平面角是关键,因为二面角确定以后,二面角的平面角很容易画出(由二面角的平面角的定义)。求角度时,常用到勾股定理、正弦定理、余弦定理、兰垂线定理和逆定理。 (2)求PE与面ECD成多少度,就是求直线与平面所成的角是多少度。首先要找出平面的一条斜线(直线PE)和斜线的射影,斜线和射影所成的锐角,就是直线PE和平面ECD所成的角,再求出角度。 设CD的中点为F,练PF,EF
∵PC=PD,EC=ED.
∴PF⊥CD,EF⊥CD(三垂线定理)
∠PFE是二面角P-CD-E的平面角
∵PE⊥PC,PE⊥CD.
∴PE⊥平面PCD,又PF在平面PCD内
∴PE⊥PF
设正方形边长为1(如图)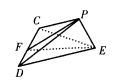
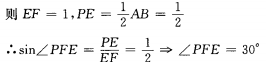 故面PCD与面ECD所成的二面角为30°,PE与面ECS成60角°。
故面PCD与面ECD所成的二面角为30°,PE与面ECS成60角°。