单选题
1、设
成等比数列,则x等于
答 案：C
解 析：由已知条件的得
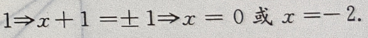
2、已知a＞b，则下列等式恒成立的是（）。
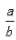＞1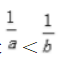
答 案：D
3、△ABC中，已知AC=12，∠A=30°，∠B=120°，则BC=（）
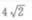
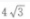
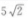
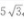
答 案：B
4、设甲：x＞3，乙：x＞5，则（）。
答 案：B
主观题
1、（1）已知tanα=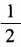
求cot2α的值； （2）已知tan2α=1，求tanα的值。
答 案：（1）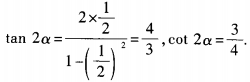
（2）由已知，得
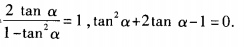解关于tanα的一元二次方程，得tanα=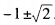
2、求下列函数的最大值、最小值和最小正周期： （1）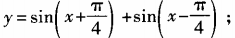
2）y=6cosx+8sinx
答 案：
所以函数的最大值是
最小值是
最小正周期为2π，
（2）要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式，需使cosx与sinx的系数平方和为1，为此，将已知函数化为
因此,函数的最大值是10,最小值是-10,最小正周期为2π
3、设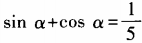
（0＜α＜π），求tanα的值。
答 案：
4、设函数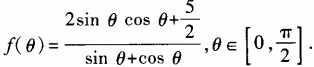
（1）求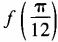
；（2）求函数f（θ）最小值。
答 案：
填空题
1、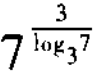
=______。
答 案：27
解 析：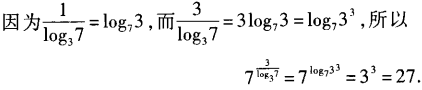
2、在1000000张奖券中，设有1个一等奖，5个二等奖，10个三等奖，从中买一张奖券，中奖的概率是______。
答 案：
解 析：本题试验属于等可能事件的概率。n=1000000，m=16，所以买一张奖券，中奖的概率
