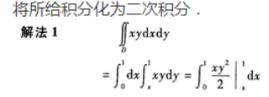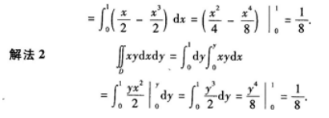单选题
1、设y=x2-3,则y’(1)=()。
答 案:B
解 析:本题考查的知识点为导数的运算。 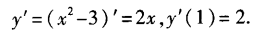 可知应选B。
可知应选B。
2、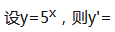 ()。
()。
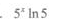
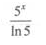
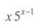
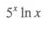
答 案:A
解 析: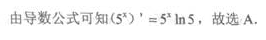
3、方程2x2+y2+z2=1表示()。
答 案:A
解 析:因为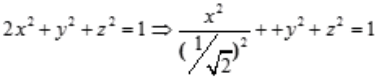 ,故该方程表示的是椭球面。
,故该方程表示的是椭球面。
主观题
1、设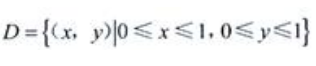 ,求
,求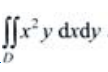 。
。
答 案:解: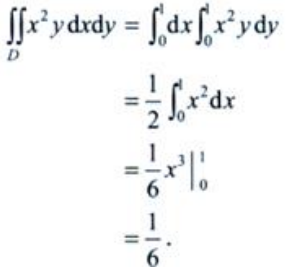
2、求曲线y=x2、直线y=2-x与x轴所围成的图形的面积A及该图形绕y轴旋转所得旋转体的体积Vy。
答 案:解:所围图形见下图。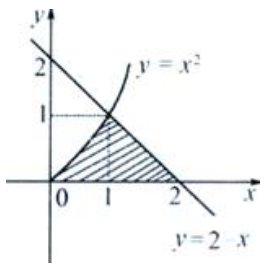
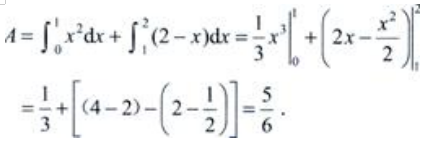 A可另求如下:由
A可另求如下:由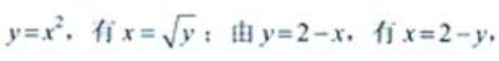 故
故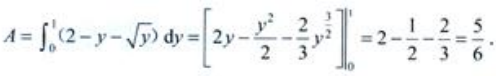
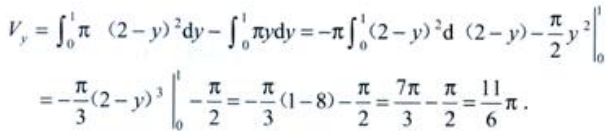
3、设函数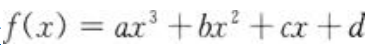 ,问常数a,b,c满足什么关系时,f(x)分别没有极值、可能有一个极值、可能有两个极值?
,问常数a,b,c满足什么关系时,f(x)分别没有极值、可能有一个极值、可能有两个极值?
答 案:解:此函数在定义域(-∞,+∞)处处可导,因此,它的极值点必是驻点即导数等于零的点,求导得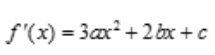 令
令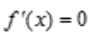 即
即 由一元二次方程根的判别式知:当
由一元二次方程根的判别式知:当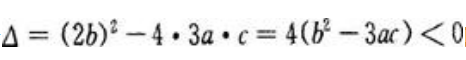 时,
时,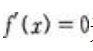 无实根。
无实根。
由此可知,当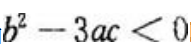 时,f(x)无极值。
时,f(x)无极值。
当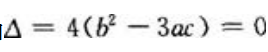 时,
时,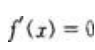 有一个实根。
有一个实根。
由此可知,当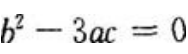 时,f(x)可能有一个极值。
时,f(x)可能有一个极值。
当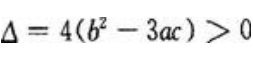 时,f(x)可能有两个极值。
时,f(x)可能有两个极值。
填空题
1、
答 案:1
解 析:

2、设z=xy,则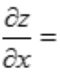 ()。
()。
答 案: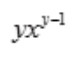
解 析: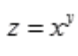 ,求
,求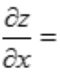 时,将y认作常量,z为x的幂函数,
时,将y认作常量,z为x的幂函数,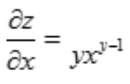 。
。
3、设z=xtan(y2+1),则 ()
()
答 案: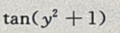
解 析:对x求偏导,可将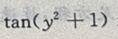 看作是常数,故
看作是常数,故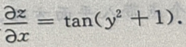
简答题
1、
答 案: