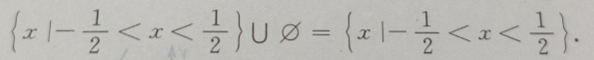单选题
1、在△ABC中，若lgsinA-lgsinB-lgcos=lg2，则△ABC是（）
答 案：B
解 析：判断三角形的形状，条件是用一个对数等式给出先将对数式利用对数的运算法则整理。 ∵lgsinA-lgsinB-lgcos=lg2，由对数运算法则可得,左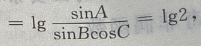
两个对数底数相等则真数相等：
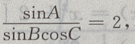即2sinBcosC=sinA
在△ABC中，∵A+B+C=180°，∴A=180°-（B+C）,
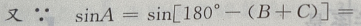
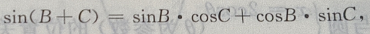
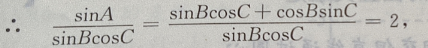
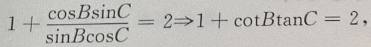
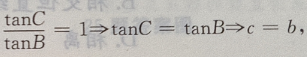故为等腰三角形
2、分别和两条异面直线AB、CD同时相交的两条直线AC、BD（）。
答 案：C
3、曲线y=x+2在点（1，2）处的切线斜率为（）。
答 案：A
解 析：方法一：∵y=x+2，k=y’＝1 方法二：也可用直线方程y=kx+b直接得出k=1。
4、如果点A(1，1)和B(2，4)关于直线y=kx+b对称，则k=（）。
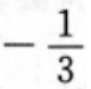
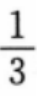
答 案：B
解 析：本题主要考查的知识点为两垂直直线斜率的关系。直线AB的斜率为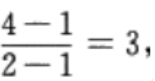
点A、B关于直线y=kx+b对称，因此直线AB与其垂直，故3k=-1，得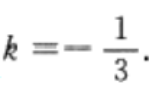
主观题
1、设
（0＜α＜π），求tanα的值。
答 案：
2、设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．
答 案：(I）f(1)=1,f'(x)=2+lnx，故f'(1)=2.所以曲线y=f(x）在点（1,f(1))处的切线方程为y=2x-1.(II）令f'(x)=0，解得
当
时，f'(x)
单调递减，在区间
单调递增．因此f(x）在
时取得极小值
3、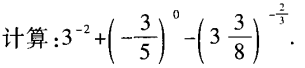
答 案：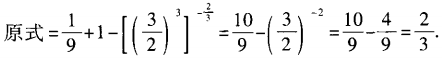
4、当自变量为何值时，函数y=2x3-3x2-12x+21有极值，其极值为多少？
答 案：y'=6x2-6x-12=6（x-2）（x+1） 当x<-1或x>2时，y>0，当-1
填空题
1、若P（3，2）是连接P1（2，y）和P2（x，6）线段的中点，则x=______，y=______。
答 案：x=4，y=-2
解 析：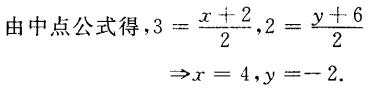
2、不等式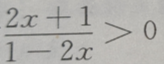
的解集为（）
答 案：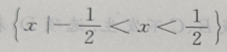
解 析：
