单选题
1、从13名学生中选出2人担任正副班长，不同的选举结果共有（）。
答 案：C
2、一批产品共有5件，其中4件为正品，1件为次品，从中一次取出2件均为正品的概率为（）。
答 案：A
解 析：本题主要考查的知识点为随机事件的概率。 一次取出2件均为正品的概率为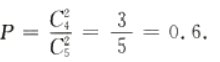
3、已知M为椭圆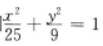
上的一点，F1,F2是椭圆的两个焦点，且∠F1MF2=60°，则△F1MF2的面积为（）
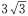
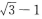
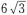
答 案：A
解 析：由椭圆方程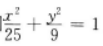
知，长轴长2a=10，焦距2c=8，设|MF1|=t，由余弦定理82=t2+（10-t）2-2t（10-t）cos60°，得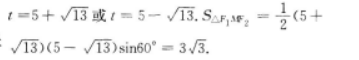
4、下列函数中，为奇函数的是（）。
答 案：D
主观题
1、设椭圆的中心是坐标原点,长轴在x轴上,离心率
已知点P
到圆上的点的最远距离是
求椭圆的方程
答 案：由题意，设椭圆方程为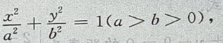
由
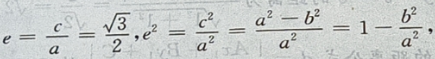
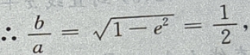设P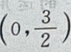
点到椭圆上任一点的距离为 d,
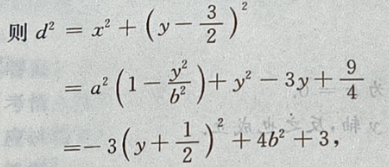
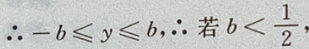则在y=-b时，
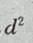最大，即d也最大。
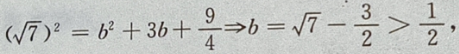
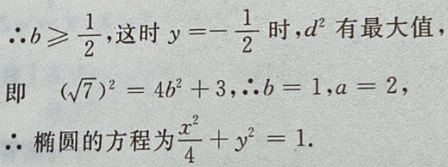
2、教室里有50人在开会，其中学生35人，家长12人，老师3人，现校长在门外听到有人在发言，那么发言人是老师或学生的概率为多少？
答 案：此题属于互斥事件，发言人是老师的概率为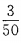
，是学生的概率为
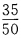，故所求概率为。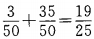
3、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)
答 案：如图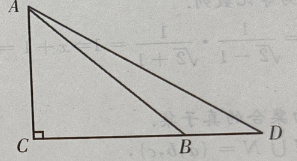 
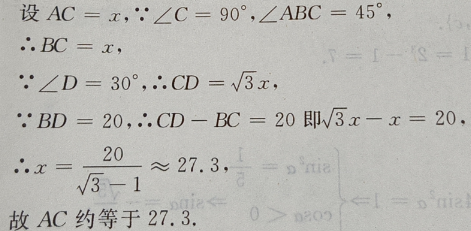
4、设函数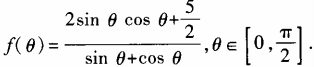
（1）求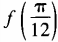
；（2）求函数f（θ）最小值。
答 案：
填空题
1、过点（2，0）作圆x2+y2=1的切线，切点的横坐标为（）。
答 案：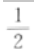
解 析：本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有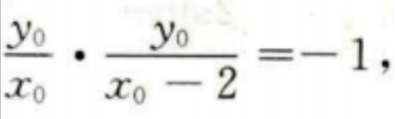
即
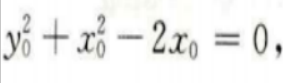
所以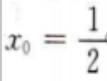
故切点横坐标为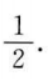
2、为了考察某种小麦的长势，从中抽取10株苗，测得苗高如下(单位：cm)：12,13，14，15，10，16，13，11，15，11． 则该品种的小麦苗高的样本方差为__________cm2．
答 案：3.6
解 析：由题中条件可得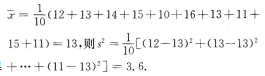
【考点指要】本题主要考查样本的平均值和方差的计算，考生只需熟记样本平均数和方差的公式即可．
