判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、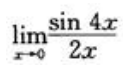 等于().
等于().
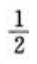
答 案:C
解 析: .
.
2、有两箱同种零件,第一箱内装50件,其中一等品10件;第二箱内装30件,其中一等品18件;现随机地从两箱中挑出一箱,再从这箱中随机地取出一件零件,则取出的零件是一等品的概率为()
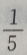
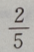
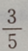
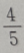
答 案:B
解 析:设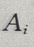 ={挑出的是第i箱},i=1,2;B={取出的是一等品},由题意知,
={挑出的是第i箱},i=1,2;B={取出的是一等品},由题意知,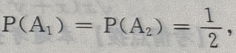
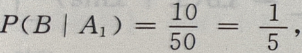
 由全概率公式知:
由全概率公式知: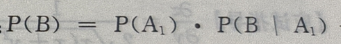 +
+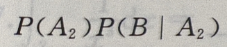
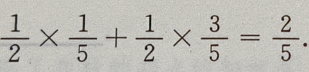
主观题
1、计算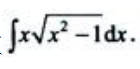
答 案:解: 
2、加工某零件需经两道工序,若每道工序的次品率分别为0.02与0.03,加工的工序互不影响,求此加工的零件是次品的概率.
答 案:解:A={第一道工序是次品),B={第二道工序是次品),C={产品是次品},则C=A+B且A与B相互独立,P(C)=P(A+B)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(A)·P(B)=0.02+0.03-0.02×0.03=0.0494.
填空题
1、 ()
()
答 案:0
解 析:令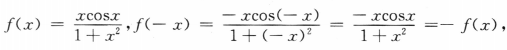 因此f(x)为奇函数,所以
因此f(x)为奇函数,所以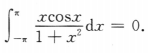
2、设函数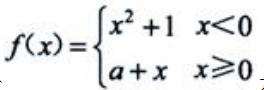 在x=0处连续,则a=().
在x=0处连续,则a=().
答 案:1
解 析:函数在x=0处连续,则有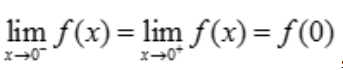 ,
,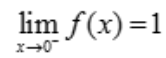 ,
,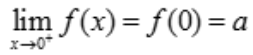 ,故a=1.
,故a=1.
简答题
1、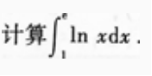
答 案: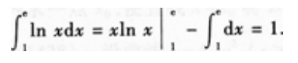
2、已知某篮球运动员每次投篮投中的概率为0.9,记X为他两次独立投篮投中的次数。①求X的概率分布;
②求X的数学期望。
答 案:①设Ai=“第i次投篮投中”(i=1,2),则两次独立投篮投中的次数X的可能取值为0,1,2。 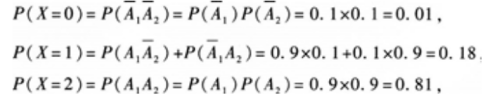 从而X的概率分布为:
从而X的概率分布为:
②E(X)=0×0.01+1×0.18+2x0.81=1.80