单选题
1、设
且
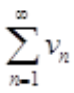收敛，则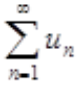
（）。
答 案：D
解 析：由正项级数的比较判定法知，若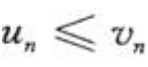
，则当
收敛时，
也收敛；若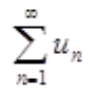
发散时，则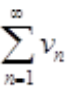
也发散，但题设未交待
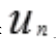与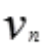
的正负性，由此可分析此题选D。
2、
（）。
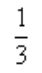
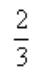
答 案：D
解 析：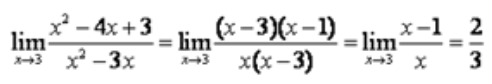
。
3、设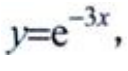
则dy＝（）。
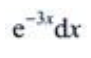
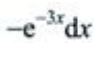
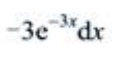
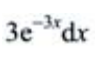
答 案：C
解 析：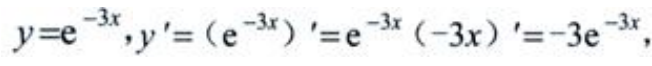
故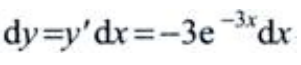
．
主观题
1、求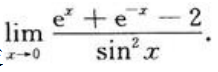
答 案：解：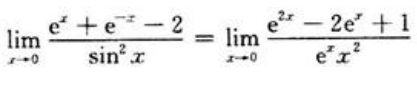
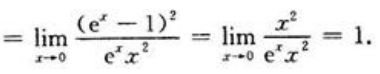
2、设
求C的值。
答 案：解：
则
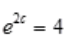，有
，
。
3、求微分方程y''－9y＝0的通解
答 案：解：特征方程为r2－9＝0，其特征根为r1＝-3，r2＝3，故通解为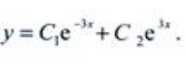
（C1，C2为任意常数）
填空题
1、设函数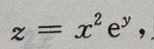
则全微分dz=（）
答 案：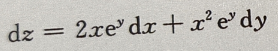
解 析：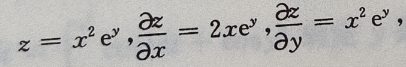
则
2、设z=ln（x2+y），则dz=（）。
答 案：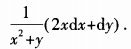
解 析：本题考查的知识点为求二元函数的全微分。 
3、过点(1,0,-1)与平面3x-y-z-2=0平行的平面的方程为（）
答 案：3x-y-z-4=0
解 析：平面3x-y-z-2=0的法向量为(3，-1，-1)，所求平面与其平行，故所求的平面的法向量为(3，-1，-1)，由平面的点法式方程得所求平面方程为3(x-1)-(y-0)-(z+1)=0，及3x-y-z-4=0。
简答题
1、求由曲线y=3-x2与y=2x，y轴所围成的平面图形的面积及该封闭图形绕x轴旋转一周所成旋转体的体积。
答 案：所给曲线围成的平面图形如图1-2所示。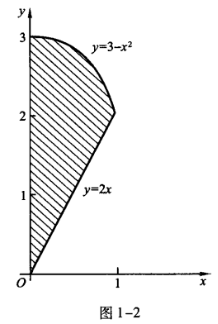 
解法1利用定积分求平面图形的面积。
解 析：本题考查的知识点有两个：利用定积分求平面图形的面积；用定积分求绕坐标轴旋转所得旋转体的体积。
