单选题

1、已知函数则f(3)等于（）。

• A：
• B：1
• C：2
• D：

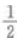
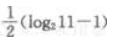
答 案：B

解 析：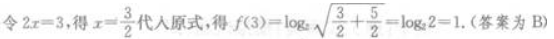

2、将一颗骰子抛掷1次,到的点数为偶数的概率为  

• A：
• B：
• C：
• D：

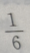
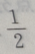
答 案：D

解 析：一颗骰子的点数分别为1,2,3,4,5,6,其中偶数与奇数各占一半,故抛掷1次,得到的点数为偶数的概率为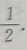

3、若x＜y＜0，则（）。  

• A：
• B：
• C：
• D：

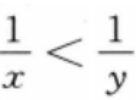
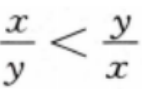
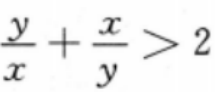
答 案：D.

解 析：本题主要考查的知识点为不等式的性质. 因为x＜y＜0，故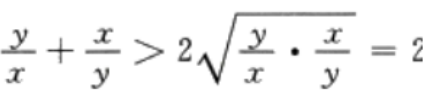

4、设（）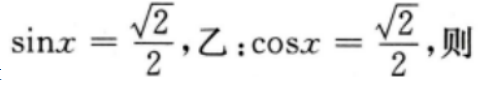

• A：甲是乙的充分条件但不是必要条件
• B：甲是乙的必要条件但不是充分条件
• C：甲是乙的充要条件
• D：甲既不是乙的充分条件也不是乙的必要条件

答 案：D

解 析：本题主要考查的知识点为简易逻辑 由于 故甲既不是乙的充分条件，也不是乙的必要条件

主观题

1、空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  

答 案：根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式所以共可确定四个平面。

解 析：空间有n个点，如果其中任何三点不在同一直线上，可以确定个平面。  

2、求函数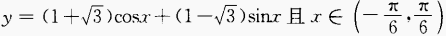上的最大值以及取得这个最大值的x。

答 案：.1 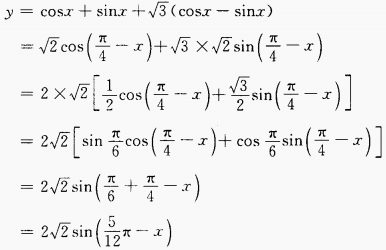函数取最大值，即y最大值=。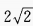

3、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。  

答 案：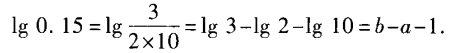

4、记△ABC的内角A，B，C的对边分别为a，b，c，已知B=60°，b²=ac，求A。    

答 案：由余弦定理b²=a²+c²-2accosB，可得ac=a²+c²-ac，即a²+c²-2ac=(a-c)²=0，解得a=c。 又因为B=60°，故△ABC为等边三角形，所以A=60°

填空题

1、ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE、CE折起，使AE与BE重合如图 ，设A与B重合后的点为P，则面PCD与面ECD所成的二面角为______度，PE与面ECD成______度。

答 案：二面角为30°，PE与面ECS成60角°  

解 析：（1）求面PCD与面ECD所成的二面角为多少度，就是要求出由平面PCD与平面ECD所组成的二面角的平面角，其中画出二面角的平面角是关键，因为二面角确定以后，二面角的平面角很容易画出（由二面角的平面角的定义）。求角度时，常用到勾股定理、正弦定理、余弦定理、兰垂线定理和逆定理。 （2）求PE与面ECD成多少度，就是求直线与平面所成的角是多少度。首先要找出平面的一条斜线（直线PE）和斜线的射影，斜线和射影所成的锐角，就是直线PE和平面ECD所成的角，再求出角度。 设CD的中点为F，练PF，EF
∵PC=PD，EC=ED.
∴PF⊥CD，EF⊥CD（三垂线定理）
∠PFE是二面角P-CD-E的平面角
∵PE⊥PC，PE⊥CD.
∴PE⊥平面PCD，又PF在平面PCD内
∴PE⊥PF
设正方形边长为1（如图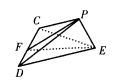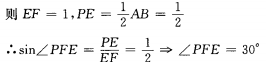） 故面PCD与面ECD所成的二面角为30°，PE与面ECS成60角°。

2、sin²10°+sin²20°+sin²40°+sin²50°+sin²70°+sin²80=______。

答 案：3

解 析：由互为余角的余函数值相等得 原式=(sin²10°+cos²10°)+(sin²20°+cos²20°)+(sin²40+cos²40)=1+1+1=3