2023年高职单招每日一练《数学》6月29日
考试总分：10分
考试类型：模拟试题
作答时间：60分钟
已答人数：571
试卷答案：有
试卷介绍： 2023年高职单招每日一练《数学》6月29日专为备考2023年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。
试卷预览
-
1. 抛物线y2=-8x的焦点坐标是(2,0).
A对
B错
-
2. 不等式x2-5x-6≤0的解集是(x|-2≤x≤3}.
A对
B错
-
1. 已知函数f(x+1)的图像过点（3,2），那么与函数f(x)的图像关于x轴对称的图形一定过点（）
A(4,2)
B(4,-2)
C(2,-2)
D(2,2)
-
2. 设a≠0,a∈R,则抛物线y=4ax2的焦点坐标为().
A(a,0)
B(0,a)
C
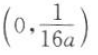
D随a符号而定
-
1. 已知两直线
,当m为何值时，l1与l2: (1)相交；(2)平行；(3)重合.
-
2. 已知函数f(x)=log3(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.
-
1. 在数列
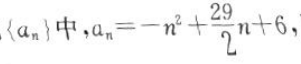则此数列最大项的值是（）。
-
2. 从五名学生中选出四名参加数学、物理、生物、化学竞赛，其中甲不参加物理和化学竞赛，则不同的参赛方案的种类是_______.
-
1. 某班有22名学生，其中正、副班长各一名，现派5名学生完成一项工作.
(1)正、副班长必须参加，有多少种派法？
(2)正、副班长只能且必须去一人，有多少种派法？
(3)正、副班长全不参加，有多少种派法？
(4)正、副班长至少有一人参加，有多少种派法？
-
2. 已知：
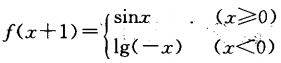，求
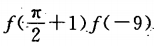的值。
相关试卷
-
2022年高职单招每日一练《数学》4月11日1399人做过
-
2022年高职单招每日一练《数学》4月12日2144人做过
-
2022年高职单招每日一练《数学》4月13日1639人做过
-
2022年高职单招每日一练《数学》4月14日1748人做过
-
2022年高职单招每日一练《数学》4月15日1240人做过
-
2022年高职单招每日一练《数学》4月16日1083人做过
-
2022年高职单招每日一练《数学》4月17日801人做过
-
2022年高职单招每日一练《数学》4月18日383人做过
-
2022年高职单招每日一练《数学》4月19日353人做过
-
2022年高职单招每日一练《数学》4月20日601人做过
相关题库
