2023年高职单招每日一练《数学》6月30日
考试总分：10分
考试类型：模拟试题
作答时间：60分钟
已答人数：1497
试卷答案：有
试卷介绍： 2023年高职单招每日一练《数学》6月30日专为备考2023年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。
试卷预览
-
1. 同时抛三枚硬币，恰有两枚硬币正面朝上的概率是
.A对
B错
-
2. 已知集合A={-1,0,1,2},B={x|x<0},则A∩B={-1,0}.
A对
B错
-
1. 若向量a=(1,1),b=(1,-1),c=(-1,2),则c等于().
A
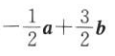
B
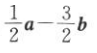
C
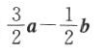
D
-
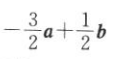
2. 已知等差数列
中，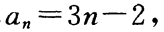
则前20项的和
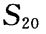（） A390
B590
C780
D295
-
1. 已知两直线
,当m为何值时，l1与l2: (1)相交；(2)平行；(3)重合.
-
2. 已知函数f(x)=log3(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.
-
1. 已知|a|=4,|b|=1,
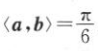,则a▪b=（）
-
2. 幂函数
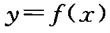的图像经过点（2,1/4），则函数的解析式是_____。
-
1.
-
2. 某蔬菜基地种植西红柿，由历年市场行情得知，从2月1日起的300天内，西红柿市场售价与上市时间的关系用图（1)的一条折线表示；西红柿的种植成本与上市时间的关系用图（2)的抛物线段表示。(1)写出图（1)表示的市场售价与时间的函数关系式P=f(t)；写出图（2)表示的种植成本与时间的函数关系式Q=g(t)；
(2)认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？
(注:市场售价和种植成本的单位:元/102kg，时间单位:天）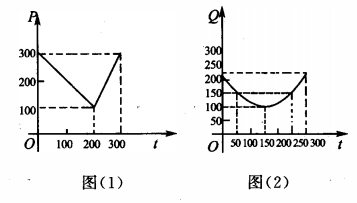
相关试卷
-
2023年高职单招每日一练《数学》11月10日1747人做过
-
2023年高职单招每日一练《数学》11月11日1638人做过
-
2023年高职单招每日一练《数学》11月12日401人做过
-
2023年高职单招每日一练《数学》11月13日1659人做过
-
2023年高职单招每日一练《数学》11月14日1121人做过
-
2023年高职单招每日一练《数学》11月15日1617人做过
-
2023年高职单招每日一练《数学》11月16日1751人做过
-
2023年高职单招每日一练《数学》11月17日417人做过
-
2023年高职单招每日一练《数学》11月18日313人做过
-
2023年高职单招每日一练《数学》11月19日486人做过
相关题库
