2024年高职单招每日一练《数学》2月2日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:1042
试卷答案:有
试卷介绍: 2024年高职单招每日一练《数学》2月2日专为备考2024年数学考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 能完全重合的两个图形成中心对称。()
A对
B错
-
2. sin2a+cos2a=1。()
A对
B错
-
1. 奇函数y=f(x),若f(2)=3,则f(-2)=()
A3
B-3
C-2
D不确定
-
2. 已知圆方程x2+y2-2x+4y-1=0的圆心为()
A(-2,4)
B(-1,2)
C(1,-2)
D(2,-4)
-
1. 设等差数列{an}的公差为d,其前n项和为Sn,且a1=-5,S3=-9,则()
Ad=2
BS2,S4,S6为等差数列
C数列
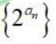 是等比数列
是等比数列DS3是Sn的最小值
-
2. 设{an}(n∈N*)是各项为正数的等比数列,q是其公比,Kn是其前n项的积,且K5K8,则下列选项中成立的是()
A0
Ba7=1
CK9>K5
DK6与K7均为Kn的最大值
-
1. 已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
-
2. 已知函数f(x)=log3(3x—1).(1)求函数f(x)的定义域;
(2)若f(x)<1,求x的取值范围.
-
1.
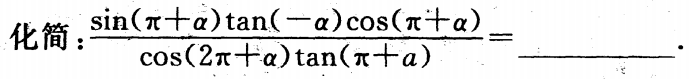
-
2. 学校文艺队每个队员唱歌、跳舞至少会一门,已知会唱歌的有5人,会跳舞的有7人,现从中选3人,且至少要有一位既会唱歌又会跳舞的概率是
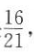 ,则该队有()人.
,则该队有()人.
相关试卷
相关题库