2024年成考高起点每日一练《数学(理)》2月15日

• 1. 给出下列两个命题：①如果一条直线与一个平面垂直，则该直线与该平面内的任意一条直线垂直②以二面角的棱上任意一点为端点，在二面角的两个面内分别作射线，则这两条射线所成的角为该二面角的平面角.则（）

  A①②都为真命题

  B①为真命题，②为假命题

  C①为假命题，②为真命题

  D①②都为假命题

• 2. 设双曲线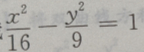的渐近线的斜率为k，则|k|=（）  

  A

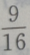
  B

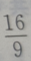
  C

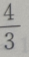
  D

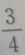
• 3. 直线3x-4y-9=0与圆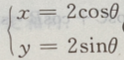(θ为参数)的位置关系是

  A相交但直线不过圆心

  B相交但直线通过圆心

  C相切

  D相离

• 4. 从椭圆与x轴额右交点看短轴两端点的视角为60°的椭圆的离心率（）  

  A

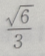
  B

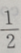
  C1

  D

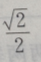
• 1. 设函数f(x)= (Ⅰ)求f(x)的单调区间; (Ⅱ)求 f(x)的极值

• 2. 设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
  (II）求f（x）的极值．

• 3. 已知a,b,c成等差数列，a,b,c+1成等比数列．若b=6，求a和c．

• 4. 已知等差数列前n项和 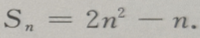（Ⅰ）求这个数列的通项公式;（Ⅱ）求数列第六项到第十项的和

• 1. 的展开式是（）

• 2. lg(tan43°tan45°tan47°)=（）