2023年高职单招考试数学真题汇编(一)
考试总分:100分
考试类型:模拟试题
作答时间:90分钟
已答人数:13036
试卷答案:有
试卷介绍: 2023年高职单招考试数学真题汇编已经整理好,需要备考的朋友们赶紧来刷题吧!
试卷预览
-
1. 下列全称量词命题与存在量词命题中:①设A、B为两个集合,若
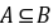 ,则对任意
,则对任意 ,都有
,都有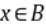 ;②设A、B为两个集合,若
;②设A、B为两个集合,若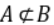 ,则存在
,则存在 ,使得
,使得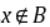 ;③
;③ 是无理数
是无理数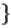 ,x2是有理数;④
,x2是有理数;④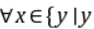 是无理数
是无理数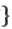 ,x3是无理数.其中真命题的个数是( )
,x3是无理数.其中真命题的个数是( )A1
B2
C3
D4
-
2. 标准对数远视力表(如图)采用的“五分记录法”是我国独创的视力记录方式,此表中各行均为正方形“E”形视标,且从视力5.2的视标所在行开始往上,每一行“”的边长都是下方一行“E”边长的10√10倍,若视力 4.2的视标边长为a,则视力5.1的视标边长为()

A
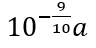
B
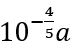
C
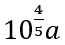
D
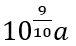
-
3. 集合A={x|1-x≤0},集合B={y|y=2x+1,x∈R},则A∩B=()
A(1,+∞)
B[1,+∞)
C(0,+∞)
Dφ
-
4. 已知集合M={x|x2-2021x≤0},N={-1,0,1,2}则集合M∩N()
A{1,2}
B{0,1,2}
C{-1,0}
Dφ
-
5. 集合A={x|1-x≤0},集合B={y|y=2x+1,x∈R}则A∩B=( )
A(1,+∞)
B[1,+∞)
C(0,+∞)
Dφ
-
6.
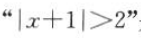 是
是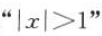 的().
的().A充分不必要条件
B必要不充分条件
C充要条件
D既不充分也不必要条件
-
7. 不等式
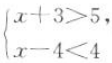 的解集为().
的解集为().A
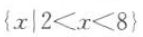
B
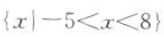
C
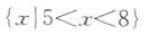
D
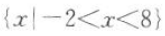
-
8. 已知
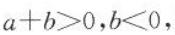 则a,b,-a,—b的大小关系是().
则a,b,-a,—b的大小关系是().Aa>b>-b>-a
Ba>-b>-a>b
Ca>b>-a>-b
Da>-b>b>-a
-
9. 若
 ,则f(-2)=().
,则f(-2)=().A4
B
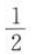
C2
D

-
10. 已知
 ,函数f(x)=x(1-x)的最大值是().
,函数f(x)=x(1-x)的最大值是().A
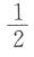
B
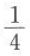
C
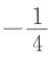
D无最大值
-
11. 已知函数
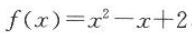 ,则f(x-1)=().
,则f(x-1)=().A

B
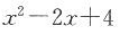
C

D

-
12. 已知
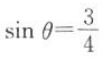 ,且θ为第二象限角,那么2θ为().
,且θ为第二象限角,那么2θ为().A第一象限角
B第二象限角
C第三象限角
D第四象限角
-
13. 已知等比数列{an} 的前n项和
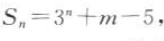 则m=()
则m=() A2
B3
C4
D5
-
14. 等比数列x,3x+3,6x+6, … 的第四项为( ).
A-24
B0
C12
D24
-
15. 已知等差数列
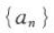 a2+a18=36,则a5+a6+ … +a15=( ).
a2+a18=36,则a5+a6+ … +a15=( ).
A130
B198
C180
D156
-
16. 数列
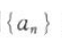 的通项公式为
的通项公式为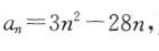 则数列
则数列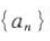 中的最小项是第()项。
中的最小项是第()项。
A4
B5
C6
D7
-
17. 下列与抛物线
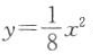 有公共焦点的双曲线为()
有公共焦点的双曲线为()A
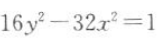
B
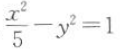
C
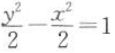
D
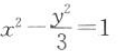
-
18. 双曲线的实轴长为a,且此双曲线上一点P到右焦点的距离也为a,则点P到此双曲线左焦点的距离为().
Aa
B2a
C3a
D4a
-
19.

A98
B99
C100
D101
-
20. 在等比数列{an} 中,若a3a6=9,a2a4a5=27,则a2的值为()
A2
B3
C4
D9
-
21. 已知集合A={-1,1},B={0,2},则集合M=(z|z=x+y,x∈A,y∈B}中的元素的个数是()。
A5
B4
C3
D2
-
22. 已知A={x|x2-3x+2=0,x∈R},
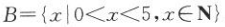 ,则满足条件A
,则满足条件A C
C B的集合C的个数为().
B的集合C的个数为().A1
B2
C3
D4
-
23. 若集合A={x|x是等边三角形},B={x|x是三角形},则下列关系中正确的是().
AA∈B
B

CA=B
D

-
24. 在直径为4的圆内接矩形中,最大的面积是()
A4
B2
C6
D8
-
25. 不等式
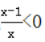 的解是()
的解是() A{x|0 < x < 1}
B{x|1 < x}
C{x|x < 0}
D{x|x < 1}
-
26. 若sina+cosa<0,tana>0,则角a的终边在()
A第一象限
B第二象限
C第三象限
D第四象限
-
27. 在下列长度的四根木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是()
A4cm
B5cm
C9cm
D13cm
-
28. 如图,△ABC中,D、E分别是边AB、AC的中点.若DE=2,则BC()
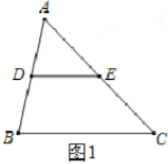
A2
B3
C4
D5
-
29. 用1,2,3,4,5,6这6个数字组成不同的六位数,所有这些六位数的平均值是( )。
A350000
B355550
C355555.5
D388888.5
-
30. 在区间[0,2]上随机取一个实数x,则事件“3x-1<0”发生的概率为()
A
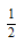
B
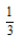
C
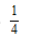
D
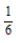
-
1. 若集合A={(x,y)|2x+ 3y-1=0},B={(x,y)|3x-2y-3=0} ,则A∩B=______。
-
2. 集合
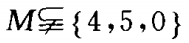 ,且M中至少有一个偶数,则这样的集合共有_____个。
,且M中至少有一个偶数,则这样的集合共有_____个。
-
3. 若指数函数的图像经过点
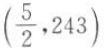 ,则其解析式为().
,则其解析式为().
-
4. 设 log37=a,则log727=__________。
-
5. 已知函数f(x)=ax3-2x的图像过点(-1,4)则a=()
-
6. 双曲线渐近线
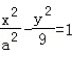 (a>0)的一条渐进线方程
(a>0)的一条渐进线方程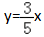 ,则a=()。
,则a=()。
-
7.
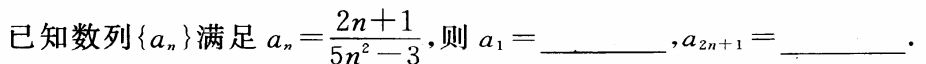
-
8. 甲、乙两射手彼此独立地射击同一目标,甲射中目标的概率为0.8,乙射中目标的概率为0.9,则恰好有一人射中目标的概率为________.
-
9.
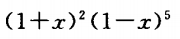 展开式中
展开式中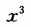 的系数为_______.
的系数为_______.
-
10. 用0,1,2,3,4,5组成没有重复数字的六位数,其中1,3,5排在一起的数的个数应是_______.
-
1. 不等式|x-3|<1的解为2<x<4。()
A对
B错
-
2. 若cosθ>0,则θ是第一象限角。()
A对
B错
-
3. 池塘里的睡莲的面积每天长大1倍,若经过17天就可以长满整个池塘,但是要长满半个池塘却需要16天。()
A对
B错
-
4. 已知函数f(x)是奇函数,且在区间[1,2]上单调递减,则f(x)在区间[-2,-1]上是单调递增函数。()
A对
B错
-
5. 函数y=1/x在(0,+∞)上单调递增。()
A对
B错
-
1. 已知集合
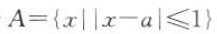 ,
,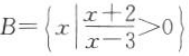 ,且A∩B=
,且A∩B= ,求实数a的取值范围.
,求实数a的取值范围.
-
2. 已知方程x2+(2k-1)x+k2=0,求方程有两个大于1的实根的充要条件.
-
3. 设x∈R,则“x3≥8”是“x2≥4”的什么条件?
-
4. 已知直线y=mx+1与双曲线
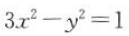 相交于P,Q两点,求m的取值范围.
相交于P,Q两点,求m的取值范围.
-
5.

-
6. 某人向某个目标射击,每次射击击中目标的概率为1/3.

-
7. 某观测点C在A地的南偏西20度方向上,从A出发有一条公路,走向是南偏东40度,在C处测得距C处31千米的公路上的B处有一个人正沿着公路向A走去,走20千米后到达D处,测的CD=21千米,这时此人距A多少千米?
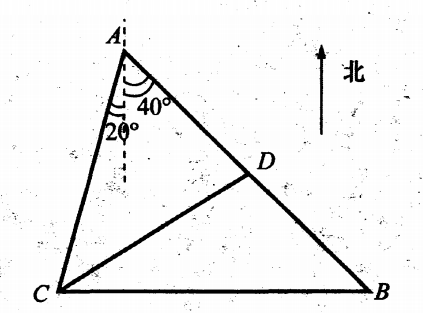
-
8. 在一块半径为R的半圆形铁板中,截取一块面积最大的矩形,则这个矩形的最大面积是多少?
-
9. 已知等差数列{an}中,a3=14,a9=-10,求S30.
-
10. 已知数列
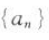 为等差数列.求证:
为等差数列.求证: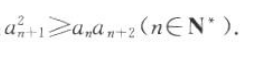
-
1. 已知函数f(x)=log3(3x—1).(1)求函数f(x)的定义域;
(2)若f(x)<1,求x的取值范围.
-
2. 已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
-
3. 已知两直线
 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
-
4. 袋中有除颜色不同外均相同的6个红色球、3个黄色球、4个黑色球、5个绿色球,现从袋中任取一个球,求取到的球不是绿球的概率.
-
5. 三名运动员练习篮球投篮,每名运动员投进的概率都是
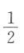 ,求在一次投篮中;(1)三名运动员同时投进的概率;
,求在一次投篮中;(1)三名运动员同时投进的概率;
(2)至少有两名运动员投进的概率.
-
2022年高职单招每日一练《数学》7月20日626人做过
-
2022年高职单招每日一练《数学》7月21日1371人做过
-
2022年高职单招每日一练《数学》7月22日1485人做过
-
2022年高职单招每日一练《数学》7月23日172人做过
-
2022年高职单招每日一练《数学》7月24日1255人做过
-
2022年高职单招每日一练《数学》7月25日114人做过
-
2022年高职单招每日一练《数学》7月26日1877人做过
-
2022年高职单招每日一练《数学》7月27日1213人做过
-
2022年高职单招每日一练《数学》7月28日1635人做过
-
2022年高职单招每日一练《数学》7月29日1608人做过