2024年成考高起点每日一练《数学(理)》5月5日

• 1. 已知空间向量i,j,k为两两垂直的单位向量，向量a=2i+3j+mk，若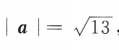，则m=（）

  A-2

  B-1

  C0

  D1

• 2. 设f(x)=x³+ax²+x为奇函数，则a=（）。

  A1

  B0

  C

  D-2 D.C.-1

• 3. 展开式中,末3项的系数(a,x 均未知) 之和为()  

  A22

  B12

  C10

  D-10

• 4. 从点M(x,3)向圆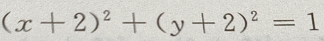作切线，切线的最小值等于（）  

  A4

  B

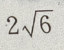
  C5

  D

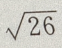
• 1. 设函数f(x)= (Ⅰ)求f(x)的单调区间; (Ⅱ)求 f(x)的极值

• 2. 在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量关于基底{a,b,c}的分解式 （Ⅱ）求证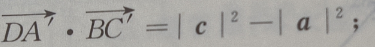： （Ⅲ）求证：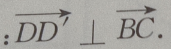  

• 3. 已知数列的前n项和 求证：是等差数列，并求公差和首项。  

• 4. 记△ABC的内角A，B，C的对边分别为a，b，c，已知B=60°，b²=ac，求A。    

• 1. 函数的定义域是（）

• 2. 长方体的长、宽、高分别为2,3,6，则该长方体的对角线长为（）