2024年成考高起点每日一练《数学(理)》5月28日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:1891
试卷答案:有
试卷介绍: 2024年成考高起点每日一练《数学(理)》5月28日专为备考2024年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1.
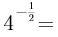 ( )
( )A-2
B
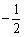
C
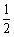
D2
-
2. 已知点M(1,2),N(2,3),则直线MN的斜率为()。
A
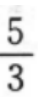
B1
C
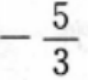
D-1
-
3. 若tanα=3,则

A-2
B
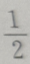
C2
D-4
-
4. 已知空间向量i,j,k为两两垂直的单位向量,向量a=2i+3j+mk,若
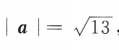 ,则m=()
,则m=()A-2
B-1
C0
D1
-
1. 在正四棱柱ABCD-A'B'C'D'中,
 (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证:
-
2. 已知数列
 的前n项和
的前n项和 求证:
求证: 是等差数列,并求公差和首项。
是等差数列,并求公差和首项。
-
3. 已知直线l的斜率为1,l过抛物线C:
 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
(II)求|AB|.
-
4. 已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。 (I)求C的方程; (Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB
-
1. 若平面向量a=(x,1),b=(1,-2),且a//b,则x=()
-
2. lg(tan43°tan45°tan47°)=()
相关试卷
-
2024年成考高起点每日一练《数学(理)》5月8日165人做过
-
2024年成考高起点每日一练《数学(理)》5月9日766人做过
-
2024年成考高起点每日一练《数学(理)》5月10日1265人做过
-
2024年成考高起点每日一练《数学(理)》5月11日430人做过
-
2024年成考高起点每日一练《数学(理)》5月12日1277人做过
-
2024年成考高起点每日一练《数学(理)》5月13日498人做过
-
2024年成考高起点每日一练《数学(理)》5月14日902人做过
-
2024年成考高起点每日一练《数学(理)》5月15日1030人做过
-
2024年成考高起点每日一练《数学(理)》5月16日1325人做过
-
2024年成考高起点每日一练《数学(理)》5月17日1684人做过
相关题库