2024年成考高起点每日一练《数学(文史)》7月10日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:2002
试卷答案:有
试卷介绍: 2024年成考高起点每日一练《数学(文史)》7月10日专为备考2024年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 设f(x)=x3+ax2+x为奇函数,则a=()。
A1
B0
C-1
D-2
-
2. 一个袋子中装有标号分别为1,2,3,4的四个球,采用有放回的方式从袋中摸球两次,每次摸出一个球,则恰有一次摸出2号球的概率为()。
A
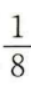
B

C
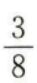
D

-
3. 已知向量a=(3,4),b=(0,-2),则cos=()
A

B
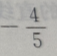
C
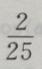
D
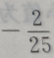
-
4. 若函数y=f(x)在[-1,1]上是单调函数,则使得y=f(sinx)必为单调函数的区间是()
AR
B[-1,1]
C

D[-sin1 ,sin1]
-
1. 设函数
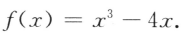
(I)求f'(2);
(II)求f(x)在区间[一1,2]的最大值与最小值.
-
2. 如图:已知在△ADC中,∠C=90°,∠D=30°,∠ABC=45°,BD=20,求AC(用小数表示,保留一位小数)

-
3. 设函数f(x)
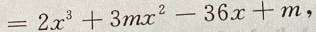 且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
-
4. 已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。(I)求C的方程;
(Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB。
-
1. 曲线在点(1,1)处的切线方程是______。
-
2. 函数
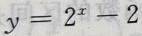 的图像与坐轴的交点共有()个
的图像与坐轴的交点共有()个
相关试卷
-
2023年成考高起点每日一练《数学(文史)》8月3日1035人做过
-
2023年成考高起点每日一练《数学(文史)》8月4日689人做过
-
2023年成考高起点每日一练《数学(文史)》8月5日482人做过
-
2023年成考高起点每日一练《数学(文史)》8月6日1796人做过
-
2023年成考高起点每日一练《数学(文史)》8月7日254人做过
-
2023年成考高起点每日一练《数学(文史)》8月8日1074人做过
-
2023年成考高起点每日一练《数学(文史)》8月9日947人做过
-
2023年成考高起点每日一练《数学(文史)》8月10日1368人做过
-
2023年成考高起点每日一练《数学(文史)》8月11日755人做过
-
2023年成考高起点每日一练《数学(文史)》8月12日1311人做过
相关题库