2024年成人高考高起点数学(文史)模拟测试试题及答案

• 1. 与圆x²+y²=4关于点M(3，2)成中心对称的曲线方程是（　）  

  A

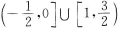
  B

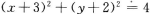
  C

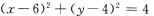
  D

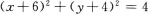
• 2. 通过点(-3，1)且与直线3x-y-3=0垂直的直线方程是（　）

  Ax+3y=0

  B3x+y=0

  Cx-3y+6=0

  D3x-y-6=0

• 3. 已知二次函数y=x²+ax+1在区间[1，+∞)上为递增函数，则实数a的取值范围是（　）

  Aa≥-2

  Ba≤-2

  Ca≥-1

  Da≤-1

• 4. （　）

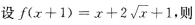  A

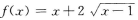
  B

  C

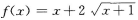
  D

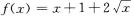
• 5. 某单位有4名男同志和3名女同志，现要组成一个有男有女的小组，规定小组中男同志的数目为偶数，女同志的数目为奇数，则共有组织方法种数是（ ）

  A18种

  B28种

  C36种

  D324种

• 6. 如果方程lg2x+(lg2+lg3)lgx+lg2×lg3=0的两个根分别是x1，x2，那么x1·x2=（　）

  Alg2×lg3

  Blg2+lg3

  C1/6

  D-6

• 7. 不等式|3x+1|≤2的解集是（　）

  A

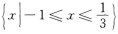
  B

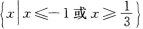
  C

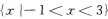
  D

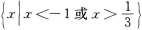
• 8. 已知sinαcosα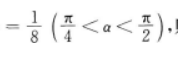则cosα-sinα的值为（）

  A

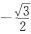
  B

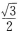
  C

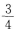
  D

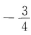
• 9. 已知|a|=4，|b|=5，向量a与b的夹角为π/3，则a·b的值为（　）

  A40

  B20

  C30

  D10

• 10. 已知函数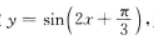，则下列命题中正确的是（　）

  A它是奇函数

  B它的图像是由y=sin2x向左平移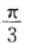得到的

  C它的图象关于直线x=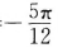成轴对称图形

  D它的单调递增区间是

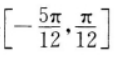
• 11. 设集合A={x|x2-2x-32}，则A∩B=（　）

  A{x|-1

  B{x|03}

  C{x|-3

  D{x|0

• 12.

  A(-∞，-6)∪(1，+∞)

  B(-6，1)

  C(-∞，2)∪(3，+∞)

  D(2，3)

• 13. 若|a|=1，|b|=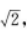（a-b）⊥a，则a与b的夹角为（　）

  A30°

  B45°

  C60°

  D75°

• 14. 下面四个关系式其中正确的个数为（）

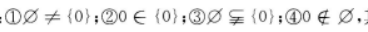
  A4

  B3

  C2

  D1

• 15. 函数的最小正周期和最大值分别为

  A

  B

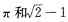
  C

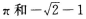
  D

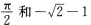
• 16. 点P(2,5)到直线x+y-9=0的距离是()

  A

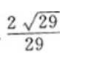
  B2

  C

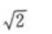
  D

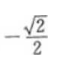
• 17. 设f(x)=1-f(x)log₂x函数，则f（2）=（）

  A1

  B-1

  C2

  D1/2

• 1. 已知tanθ=1/2，则sin2θ+sin2θ=__________．

• 2. 为了考察某种小麦的长势，从中抽取10株苗，测得苗高如下(单位：cm)：12,13，14，15，10，16，13，11，15，11． 则该品种的小麦苗高的样本方差为__________cm2．

• 3. 某学科的一次练习中，第一小组5个人成绩如下(单位：分)：98，89，70，92，90，则分数的样本方差为__________．

• 4. 在∆ABC中，已知cosA=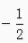，cosB=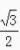，那么cosC=______。

• 1. 已知函数ƒ(x)=ax3-x2+bx+1(a，b∈R)在区间(-∞，0)和(1，+∞)上都是增函数，在(0，1)内是减函数． (Ⅰ)求a，b的值； (Ⅱ)求曲线y=ƒ(x)在x=3处的切线方程．

• 2. 若双曲线的两条准线将两个焦点的连线分成三等分,求双曲线的离心率。

• 3. 已知F是椭圆的右焦点，点M在抛物线y2=2px（p＞0）上O为坐标原点，且△MOF为正三角形．  (Ⅰ)求P的值； (Ⅱ)求抛物线的焦点坐标和准线方程．

• 4. 若tanα、tanβ是关于x的方程mx²-(2m-3)x+m-2=0的两个实根，求tan(α+β)的取值范围