2024年成人高考高起点数学(理)模拟试卷及答案(一)

• 1. 设集合M＝{0，1，2，3，4}，N＝{1，2，3}，T＝{2，4，6}，则集合（M∩T）∪N＝（）。  

  A{0，1，2，3，4，6}

  B{1，2，3，4}

  C{2，4}

  D{2，4，6}

• 2. 已知两条异面直线m；n，且m在平面α内，n在平面β内，设甲：m//β，n//α；乙：平面α//平面β，则（）。

  A甲为乙的必要但非充分条件

  B甲为乙的充分但非必要条件

  C甲非乙的充分也非必要条件

  D甲为乙的充分必要条件

• 3. 设甲：二次不等式x²+px+q＞0的解集为空集合；乙：△=p²-4q＜0则（）。

  A甲是乙的必要条件，但不是乙的充分条件

  B甲是乙的充分条件，但不是乙的必要条件

  C甲不是乙的充分条件，也不是乙的必要条件

  D甲是乙的充分必要条件

• 4. 下列关系式中，对任意实数A＜B＜0都成立的是（）。

  Aa²＜b²

  Blg(b－a)＞0

  C2^a＜2^b

  Dlg(-a)＜lg(－b)

• 5. 函数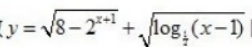的定义域为（）。

  A{x|x>1}

  B{x|x≤2}

  C{x|1

  D{x|1

• 6. 在点x＝0处的导数等于零的函数是（）。

  Ay＝sinx

  By＝x－1

  Cy＝ex－x

  Dy＝x²－x

• 7. 函数y＝lg(x²－3x＋2)的定义域为（）。

  A{x|x＜1或x＞2}

  B{x|1＜x＜2}

  C{x|x＜1}

  D{x|x＞2}

• 8. 若f(x＋1)＝x²－2x＋3，则f(x)＝（）。

  Ax²＋2x＋6

  Bx²＋4x＋6

  Cx²－2x＋6

  Dx²－4x＋6

• 9. 三个数0，3^0.7，log₃0.7的大小关系是（）。

  A0＜3^0.7＜log₃0.7

  Blog₃0.7＜0＜3^0.7

  Clog₃0.7＜3^0.7＜0

  D0＜log₃0.7＜3^0.7

• 10. 正三棱柱的每条棱长都是a，则经过底面一边和相对顶点的截面面积是（）。

  A

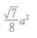
  B

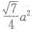
  C

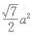
  D

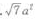
• 11. 在正方体ABCD-A’B’C’D’中，△A’BC的形状是（）。

  A等腰三角形

  B等边三角形

  C直角三角形

  D等腰直角三角形

• 12. (sinα+sinβ)²+(cosα+cosβ)²=（）。

  A

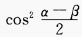
  B

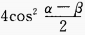
  C

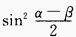
  D

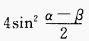
• 13. 若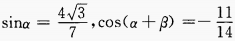，且α、β均为锐角，则β的值为（）。

  A

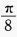
  B

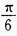
  C

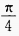
  D

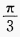
• 14. （）。

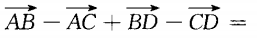  A0

  B

  C

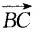
  D

• 15. 从1、2、3、4、5、6、7、8、9这九个数字中，随机取出一个数字，这个数字是奇数的概率是（）。

  A

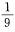
  B

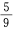
  C

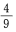
  D

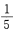
• 16. =（）。

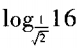  A8

  B-8

  C2

  D-2

• 17. 函数y=sinx+cosx（x∈R）的最小正周期为（）。

  A2π

  Bπ

  C

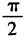
  D

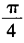
• 1. 已知A（0,1），B（1，2），存在一点P是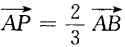，则点P的坐标是______。

• 2. 与已知直线 7x+24y-5 =0 平行，且距离等于3的直线方程是______。  

• 3. 已知关于t的二次方程t2-6tsinθ+tanθ=0（0＜θ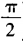＜）的两根相等，则sinθ+cosθ的值等于______。

• 4. 函数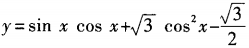（x∈R）的最小值为______。

• 1. 已知数列{a_n}中，a₁=2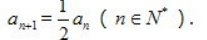， （Ⅰ）求数列{a_n}的通项公式; （Ⅱ）求数列{a_n}前5项的和 S₅

• 2. 空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  

• 3. 已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。

• 4. 设函数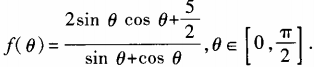（1）求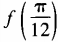；（2）求函数f（θ）最小值。