2024年成考专升本高等数学一模拟习题(二)

• 1. 设x是f（x）的一个原函数，则f（x）=（）。  

  A

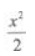
  B

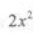
  C1

  DC（任意常数）

• 2. 设f（x）在[a，b]上连续，x∈[a，b]，则下列等式成立的是（）。  

  A

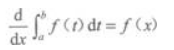
  B

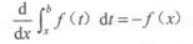
  C

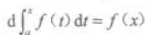
  D

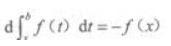
• 3. 设f（x）在点x=2处连续，（）。  

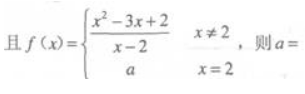  A0

  B1

  C2

  D任意值

• 4. （）。  

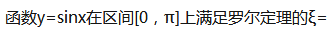  A0

  B

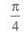
  C

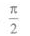
  D

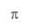
• 5. （）。  

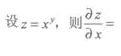  A

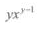
  B

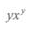
  C

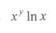
  D

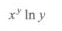
• 6. （）。  

  A

  B

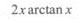
  C

  D

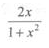
• 7. （）。  

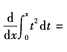  Ax²

  B2x²

  Cx

  D2x

• 8. （）。  

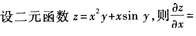  A2xy+siny

  Bx²+xcosy

  C2xy+xsiny

  Dx²y+siny

• 9. （）。  

  A收敛且和为0

  B收敛且和为a

  C收敛且和为a-a₁

  D发散

• 1.  

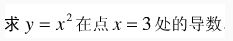
• 2.  

• 3. 设x²为f（x）的一个原函数，则f（x）=_____。  

• 4. 过原点且与平面2x-y+3z+5=0平行的平面方程为______。  

• 5.  

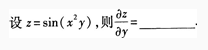
• 6. 设函数z=ln（x+y²），则全微分dz=_______.  

• 7.  

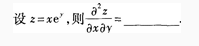
• 8. 过点M₀（1，-2，0）且与直线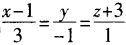垂直的平面方程为（）。  

• 9. 设z=ln（x²+y），则dz=（）。  

• 1.  

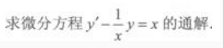
• 2.  

• 3.  

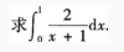
• 4. 设曲线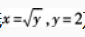及x=0所围成的平面图形为D。（1）求平面图形D的面积s。
  （2）求平面图形D绕y轴旋转一周生成的旋转体体积V  

• 5.  

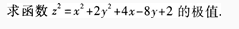
• 6. 研究级数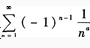的收敛性（即何时绝对收敛，何时条件收敛，何时发散，其中常数a>0。  

• 7.  

• 8. 求微分方程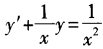的通解。